Погрешность, возникающая при замене значения функции 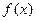 значением интерполяционного многочлена
значением интерполяционного многочлена 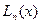 , представима формулой:
, представима формулой:
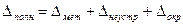 .
.
Слагаемые 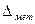 метода и
метода и 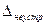 вычисляются теоретически,
вычисляются теоретически, 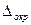 можно получить лишь в самом процессе счета, так как погрешность округления зависит от того, как ведутся вычисления.
можно получить лишь в самом процессе счета, так как погрешность округления зависит от того, как ведутся вычисления.
А. Оценка погрешности метода (погрешности интерполирования).
Займёмся оценкой величины 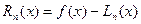 , считая, что многочлен
, считая, что многочлен 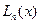 построен по точным данным и что значения его вычисляются абсолютно точно.
построен по точным данным и что значения его вычисляются абсолютно точно.
Теорема. Если в промежутке, содержащем все узлы интерполяции, функция 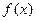 имеет (n+1)-ую ограниченную производную, то для любого значения
имеет (n+1)-ую ограниченную производную, то для любого значения 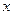 из этого промежутка
из этого промежутка
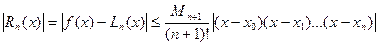 .
.
То есть
 , (4)
, (4)
где Мn+1 -верхняя граница значений 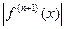 на рассматриваемом промежутке.
на рассматриваемом промежутке.
Доказательство.
Рассмотрим вспомогательную функцию
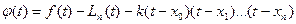 ,
,
где к -некоторое число. Функции f(t) и 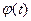 имеют производные до (n+1)-го порядка. Функция
имеют производные до (n+1)-го порядка. Функция 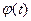 обращается в нуль во всех узлах интерполяции
обращается в нуль во всех узлах интерполяции 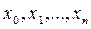 :
:
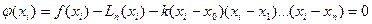
Для данного значения x ≠ xi, отличного от всех узлов интерполяции, подберём число к, так чтобы 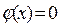 . Для определения числа к получаем условие
. Для определения числа к получаем условие
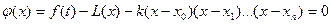
Поскольку 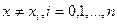 , то множитель при числе к отличен от нуля и получаем:
, то множитель при числе к отличен от нуля и получаем:
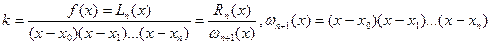
Вычислим теперь число к другим способом. С этой целью вспомним теорему Ролля: между каждыми двумя нулями дифференцируемой функции имеется хотя бы один нуль её производной. Функция 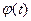 имеет (n+2) нуля
имеет (n+2) нуля 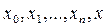 . Следовательно, её производная
. Следовательно, её производная 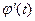 имеет, по крайней мере (n+1) нуль. Применяя повторно теорему Ролля к производной
имеет, по крайней мере (n+1) нуль. Применяя повторно теорему Ролля к производной 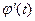 , убеждаемся в том, что вторая производная
, убеждаемся в том, что вторая производная 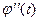 имеет, по крайней мере, n нулей. Продолжая, получим, что (n+1) -ая производная
имеет, по крайней мере, n нулей. Продолжая, получим, что (n+1) -ая производная 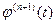 имеет, по крайней мере, один нуль, т.е. найдётся точка ξ, в которой
имеет, по крайней мере, один нуль, т.е. найдётся точка ξ, в которой
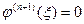
Найдём производную 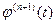 :
:
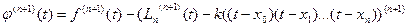
Производная (n+1)-го порядка от многочлена n -ой степени равна нулю, то 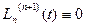
Вычислим (n+1)-ую производную, входящую в последнее слагаемое:
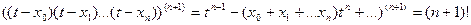 .
.
Следовательно, 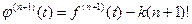
В точке ξ имеем: 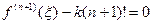 ,т.е.
,т.е. 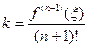
Сравнивая два выражения для числа к, получаем 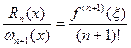
Таким образом, в наших условиях найдётся точка ξ, такая что 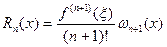
В полученной формуле число ξ неизвестно, поэтому она не может быть использована на практике. Получим формулу, которую можно использовать на практике. Значения 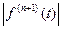 ограничены числом
ограничены числом 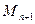 , тем самым
, тем самым 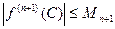 .
.
Следовательно, 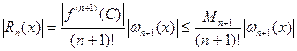 .
.
В. Оценка неустранимой погрешности.
При получении интерполяционного многочлена Лагранжа
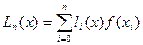
Вместо точных значений функции 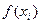
 использованы приближённые значения
использованы приближённые значения 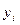 , т.е. вместо требуемого многочлена
, т.е. вместо требуемого многочлена 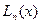 получен многочлен
получен многочлен 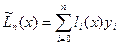
Неточность исходных данных 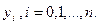 , приводит к неустранимой погрешности
, приводит к неустранимой погрешности 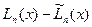 . Считая известной абсолютную погрешность
. Считая известной абсолютную погрешность 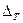 значений
значений 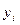 :
: 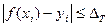 :
:
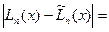
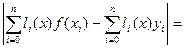
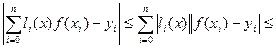
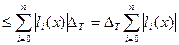 ,
,
следовательно,
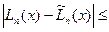
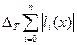
Абсолютная неустранимая погрешность равна
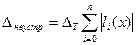
С. Полная погрешность формулы Лагранжа.
Объединяя полученные результаты, можно написать следующее выражение для полной погрешности формулы Лагранжа
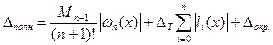 , (4)
, (4)
где 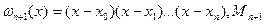 - верхняя граница значений
- верхняя граница значений 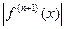 на рассматриваемом отрезке;
на рассматриваемом отрезке; 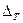 - абсолютная погрешность вычисления значения функции
- абсолютная погрешность вычисления значения функции 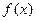 ;
; 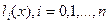 -многочлены;
-многочлены; 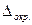 - суммарная погрешность всех проведённых в ходе вычисления округлений.
- суммарная погрешность всех проведённых в ходе вычисления округлений.
Пример 10.
Для функции 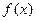 = sin(x) сузлами
= sin(x) сузлами 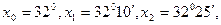 построен интерполяционный многочлен Лагранжа
построен интерполяционный многочлен Лагранжа 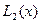 . Вычислить значение многочлена при
. Вычислить значение многочлена при 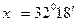 и оценить полную погрешность, считая, что использованы пятизначные таблицы значений sin(x) (т.е.
и оценить полную погрешность, считая, что использованы пятизначные таблицы значений sin(x) (т.е. 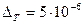 ). Вычислим значение
). Вычислим значение 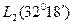 :
:
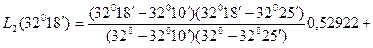
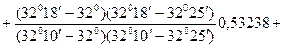
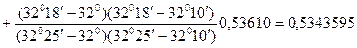 .
.
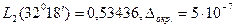
Оценим погрешность интерполирования: 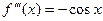 и на отрезке от
и на отрезке от 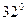 до
до 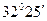 имеем
имеем 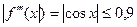 , т.е.
, т.е. 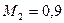 .
.
В формуле для вычисления погрешности интерполирования значения 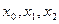 и
и 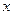 переведем в радианы, получим
переведем в радианы, получим
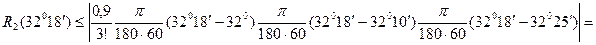
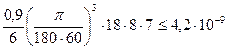
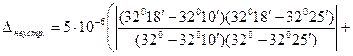
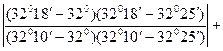
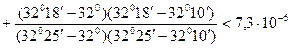 .
.
Таким образом,
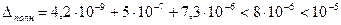 ,
,
Следовательно, 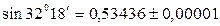 .
.
 2015-01-21
2015-01-21 7345
7345
