Каждому узлу интерполяции 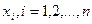 , сопоставим многочлен
, сопоставим многочлен
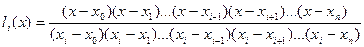 . (1)
. (1)
Многочлен 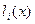 равен нулю в любом узле интерполяции
равен нулю в любом узле интерполяции 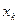 , отличном от узла
, отличном от узла 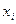 , так как в числителе имеется множитель
, так как в числителе имеется множитель 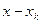 , который обращается в нуль при
, который обращается в нуль при 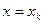 .
.
В узле 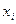 многочлен
многочлен 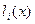 принимает значение равное единице, так как при
принимает значение равное единице, так как при 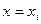 числитель и знаменатель совпадают
числитель и знаменатель совпадают 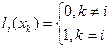 ,
,
Докажем, что интерполяционный многочлен 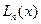 можно представить формулой:
можно представить формулой:
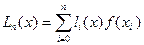 (2).
(2).
Правая часть равенства (2) является многочленом степени не выше n. В узлах интерполяции 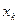 её значение равно:
её значение равно:
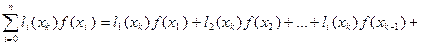
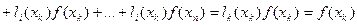 ,
,
при 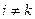 все числа
все числа 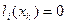 , а при
, а при 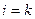
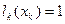 . Многочлен представленный формулой (2), удовлетворяет всем условиям задачи. Формула (2) называется интерполяционной формулой Лагранжа в развернутой форме:
. Многочлен представленный формулой (2), удовлетворяет всем условиям задачи. Формула (2) называется интерполяционной формулой Лагранжа в развернутой форме:
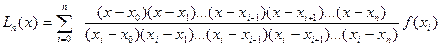 (3)
(3)
или
Ln (x)= 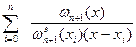 f (xi)
f (xi)
где
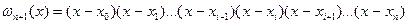 ,
,
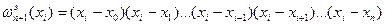 .
.
Теорема. Задача интерполяции всегда имеет единственное решение, которое может быть представлено формулой (3).
Пример 9. Пользуясь формулой Лагранжа, составить интерполяционный многочлен по условиям примера 7. В этом случае 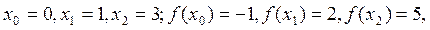
Формула (3) даёт:
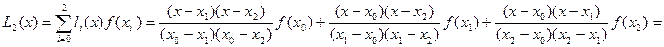
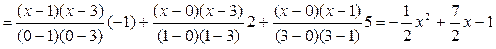 .
.
 2015-01-21
2015-01-21 1634
1634
