Конечная разность первого порядка функции f(x) при шаге h>0 определяется равенством
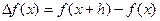 (6)
(6)
Разности высших порядков определяются индуктивно: разность (к+1) – порядка есть разность первого порядка от разности к-го порядка:
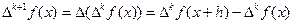
Например,
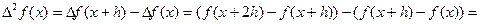
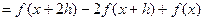
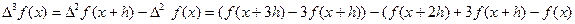
Методом индукции можно установить общую формулу.
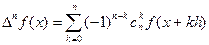 , (7)
, (7)
Значение разности 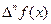 полностью определяется значениями функции f(x) в точках x,x+h,…,x+nh.
полностью определяется значениями функции f(x) в точках x,x+h,…,x+nh.
Вычисление разностей производится по таблице значений функции. При этом конечную разность в точке x записывают между значениями функции в точках x и x+h. Получение разностей показано в таблице:
| x | f(x) | 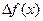 | 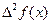 | 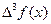 |
| x | 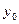 | 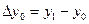 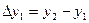 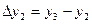 | 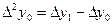 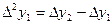 | 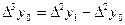 |
| x + h | 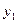 | |||
| x +2h | 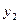 | |||
| x +3h | 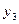 |
Свойства конечных разностей:
1. Конечная разность от постоянной величины равна нулю.
2. Операция вычисления конечной разности является линейной, т.е. для 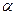 ,
, 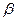
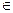 R:
R:
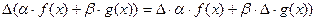
Доказательство:
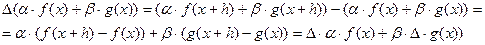
Cвойство верно для разностей любого порядка.
3. Конечной разностью от многочлена степени n является многочлен степени (n-1), т.е. при вычислении разности, степень многочлена понижается на единицу.
С учётом предыдущего свойства достаточно доказать это свойство для 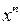 .
.
Имеем:
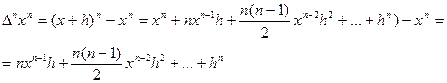
4. Конечная разность n -го порядка от многочлена n -ой степени постоянна, все разности более высокого порядка равны нулю.
Доказательство свойства следует из предыдущего.
5. Для многочлена 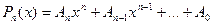 справедлива формула:
справедлива формула:
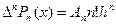
Применяя последовательно формулу из доказательства свойства 3, получим
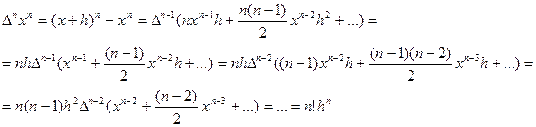
Следовательно, для многочлена 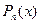 получим
получим
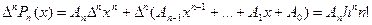
Поскольку по свойству 4:
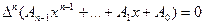
Без доказательства сформулируем следующее свойство.
5. Если функция f(x) имеет непрерывную в точке x производную к -ого порядка, то 
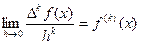
Следовательно, при малых справедливо приближенное равенство 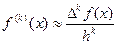
Приведённая формула дает грубое приближение вследствие малого числа 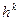 в знаменателе. Например, если вычисляется производная
в знаменателе. Например, если вычисляется производная 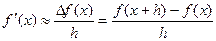 и погрешность вычисления значения функции равна
и погрешность вычисления значения функции равна 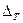 , то возникающая из-за этого неустранимая погрешность равна
, то возникающая из-за этого неустранимая погрешность равна 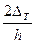 . При h=0,1;0,01;0,001 получаются ошибки
. При h=0,1;0,01;0,001 получаются ошибки 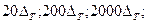 .
.
 2015-01-21
2015-01-21 9510
9510
