Пределы допускаемой основной погрешности средства измерения

Максимальная основная погрешность СИ, при котором он разрешен к применению, называется пределом допускаемой основной погрешности.

Пределы допускаемой основной погрешности устанавливают как 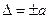или 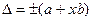, где х – значение измеряемой величины, а и b – положительные числа, не зависимые от х.

Первая формула описывает аддитивную погрешность, вторая – сумму аддитивной и мультипликативной погрешностей СИ.

Графическое представление этих погрешностей приведены ниже.

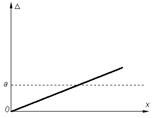
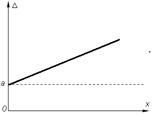
а) б) в) г)

Виды погрешностей средств измерений

а – аддитивная, б – мультипликативная,

в – сумма аддитивной и мультипликативной, г – относительная суммарная

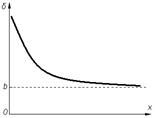
При проведении измерений важное значение имеет выбор диапазона измерений СИ, что хорошо видно на графике относительной суммарной погрешности δ. При уменьшении измеряемой величины относительная погрешность δ увеличиваетсяи изменяется по гиперболе. Поэтому следует выбирать такой диапазон измерений, в котором значение измеряемого параметра близко к большему (по модулю) из пределов измерений.

Следует подчеркнуть, что представленные выше графики выполнены для положительных погрешностей, но погрешности могут иметь любой знак. Поэтому в общем случае выражения абсолютной и относительной погрешностей СИ записываются со знаком «±».

В формулах пределов допускаемой основной погрешности значения ∆ и х выражаются одновременно либо в единицах измеряемой или воспроизводимой мерой величины, либо в делениях шкала средства измерения. В этих случаях класс точности обозначается заглавными буквами латинского алфавита (например, H,I,K,L,M и т.д.) или римскими цифрами (I,II,..IV). К буквам при этом допускается присоединять индексы в виде арабских цифр. Чем меньше пределы допускаемой погрешности, тем ближе к началу алфавита должна быть буква и тем меньше цифра.

Пределы допускаемой приведенной основной погрешности устанавливают по формуле γ = 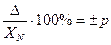. Здесь Х_N – нормирующее значение, выраженное в тех же единицах, что и абсолютная погрешность ∆; р – отвлеченное положительное число, выбираемое из ряда предпочтительных чисел: 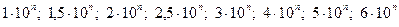, где 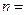1, 0, -1, -2, -3 и т.д.

Для средств измерений с равномерной, практически равномерной или степенной шкалой значение Х_N принимают равным:

· Большему из пределов измерений, если нулевое значение (нулевая метка) находятся на краю или за пределами диапазона измерений;

· Сумме модулей пределов измерений, если нулевое значение находится внутри диапазона измерений.

Пределы допускаемой относительной основной погрешности записываются как δ = 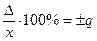, если погрешность только аддитивная, т.е 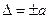. Здесь q – отвлеченное положительное число, выбираемое из ряда предпочтительных чисел.

Если формула погрешности включает в себя аддитивную и мультипликативную части, т.е 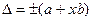, пределы допускаемой относительной основной погрешности записываются как 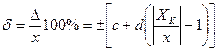, где с – суммарная погрешность прибора; d –аддитивная относительная погрешность прибора; Х_К – конечное значение диапазона измерений.

Величины с и d выбираются из ряда предпочтительных чисел.

Величины а, b, c, d в формулах ∆ и δ связаны между собой следующим образом: 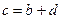, , 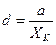причем всегда .

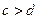Классы точности измерительных приборов, пределы допускаемой относительной основной погрешности которых принято выражать в виде дольного значения предела допускаемой основной погрешности. Принято обозначать числами с и d (в процентах), разделяя их косой чертой (например, 0,05/0,02).

Предел допускаемой абсолютной дополнительной погрешности измерения может указываться в виде:

· Постоянного значения для всей рабочей области влияющей величины млм посиоянных значений по интервалам рабочей области влияющей величины;

· Отношения предела допускаемой дополнительной погрешности, соответствующего регламентированному интервалу влияющей величины, к этому интервалу.

· Зависимости предела 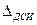от влияющей величины.