1. Каким условиям должна удовлетворять функция на отрезке, чтобы на нем находился единственный корень?
2.Что заносится в таблицу исходных данных для реализации рассматриваемого метода?
3. По какому правилу производится сужение отрезка после нахождения его середины?
4. Какой критерий остановки используется? Как фиксируется и доводится до сведения пользователя факт необходимости остановки?
5. Могут ли быть исключены из указанной выше таблицы какие - либо столбцы с избыточными вычислениями?
6. Какая точка внутри последнего отрезка может быть принята за окон-чательное решение?
7. Как аналитически найти наибольшее требуемое число шагов при известном от-резке неопределенности и заданной предельной абсолютной погрешности?
ЗАДАНИЕ 2. МЕТОД ХОРД ДЛЯ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
2-1. Отделить один из корней уравнения 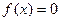 . На основе анализа знаков
. На основе анализа знаков 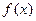 и
и 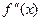 на границах найденного отрезка неопределенности
на границах найденного отрезка неопределенности 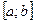 определить неподвижную границу. Уточнить корень методом хорд, сдвигая одну из границ отрезка, за число шагов
определить неподвижную границу. Уточнить корень методом хорд, сдвигая одну из границ отрезка, за число шагов 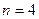 . Оценить абсолютную
. Оценить абсолютную 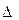 и относительную
и относительную 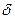 погрешности для полученного решения. Построить график изменения этих погрешностей в зависимости от числа шагов i.
погрешности для полученного решения. Построить график изменения этих погрешностей в зависимости от числа шагов i.
2-2. Отделить один из корней уравнения 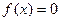 . Уточнить корень методом хорд с абсолютной погрешностью не более
. Уточнить корень методом хорд с абсолютной погрешностью не более 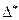 = 0,0001 и с относительной погрешностью, не превышающей предельное значение
= 0,0001 и с относительной погрешностью, не превышающей предельное значение 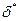 = 0,05%. Построить графики изменения абсолютной
= 0,05%. Построить графики изменения абсолютной  и относительной
и относительной 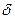 погрешностей в зависимости от числа шагов i. Определить число шагов вычислительного процесса для достижения требуемой точности.
погрешностей в зависимости от числа шагов i. Определить число шагов вычислительного процесса для достижения требуемой точности.
Варианты исходных уравнений представлены ниже.
| Вариант | Уравнение 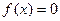
|
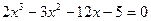
| |
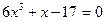
| |
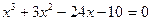
| |
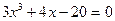
| |
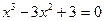
| |
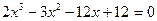
| |
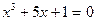
| |
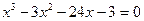
| |
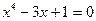
| |
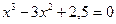
| |

| |
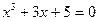
| |
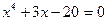
| |

| |
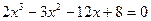
| |
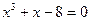
| |

| |
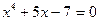
| |
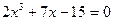
| |
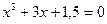
| |
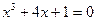
| |
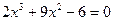
| |
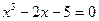
| |

| |
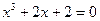
| |
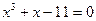
| |
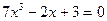
| |
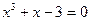
| |

| |
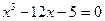
| |

| |
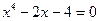
| |
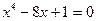
| |
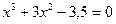
| |
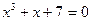
|
 2015-01-21
2015-01-21 353
353








