Наращение по непрерывной дискретно изменяющейся процентной ставке

Период	Наращенная сумма к концу периода
	S
t1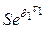
t2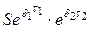
t3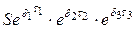
…	…
tk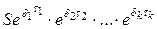

2. Сила роста непрерывно изменяется во времени и описывается линейным уравнением

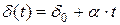, (37)

где d₀ — начальная сила роста (при t=0);

a — годовой прирост (снижение), может быть больше или меньше нуля.

Так как 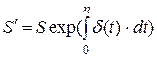, возьмем следующий интеграл:

.

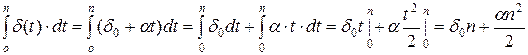Тогда 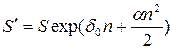(38)

— наращение по непрерывной ставке, изменяющейся во времени по линейному закону;

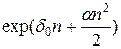(39)

— множитель наращения по непрерывной процентной ставке, изменяющейся по линейному закону.

1. Сила роста непрерывно изменяется по геометрической прогрессии.

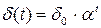, (40)

где d₀ — начальная сила роста;

a — годовой коэффициент роста (знаменатель геометрической прогрессии).

Тогда ;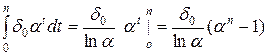

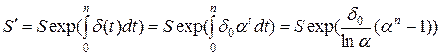(41)

— наращение по непрерывной процентной ставке, изменяющейся в геометрической прогрессии;

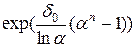(42)

— множитель наращения по непрерывной процентной ставке, изменяющейся в геометрической прогрессии.

Задачи