Скоростное поле сплошной среды в окрестности точки. Первая теорема Гельмгольца

Чтобы детальнее изучить механизм движения сплошной среды, применим приём разложения движения на составляющие, а именно первое движение элементарного объёма среды без деформации (как абсолютно твёрдого) и второе деформационное движение элементарного объёма среды. В случае сплошной недеформируемой среды движение «твёрдого» тела любого размера можно рассматривать как состоящее из поступательного его движения вместе с некоторым произвольно выбранным в нём полюсом 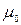и вращения вокруг мгновенной оси, проходящей через выбранный полюс 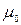с одинаковой для всех точек недеформированной среды угловой скоростью .

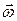Если 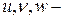составляющие вектора движения произвольной точки М этого тела, т.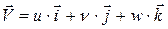е. , где 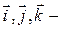орты некоторой неподвижной прямоугольной системы координат 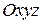, 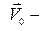вектор скорости полюса 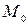. 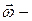вектор угловой скорости вращения объёма. 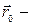радиус – вектор полюса т. 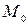. 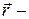радиус вектор точки 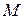. То из кинематики твёрдого тела нам известно, что

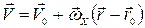(1)

А в проекциях на оси координат:

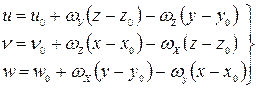(2)

Возьмём производные от 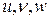по координатам 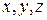при фиксированных значениях 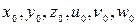и :

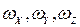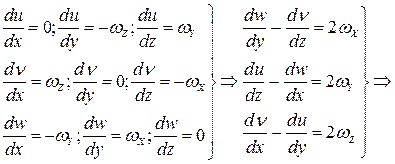
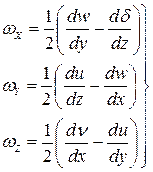(3)

В общем случае деформируемой среды также можно разложить движение на отдельные составляющие (поступательное вместе с полюсом т. и вращательное вокруг оси проходящей через т. ), но в отличие от абсолютно твёрдой среды вектор угловой скорости уже не будет одинаковым для всех точек среды и приходится рассматривать разложение движения среды только в малом, элементарном её объёме в окружности данной точки 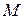. Пусть т. 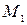лежит в элементарном объёме вблизи т. 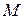, тогда направленный отрезок 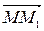- можно рассматривать как малый (элементарный) 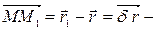дифференциал для фиксированного момента времени (поэтому вместо символа 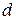стоит ).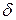

Т.к. 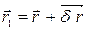, то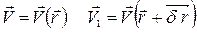

Разлагая, в ряд Тейлора, и откладывая малые величины второго и высшего порядка малости, получим:

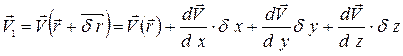
Или в проекциях на оси координат:

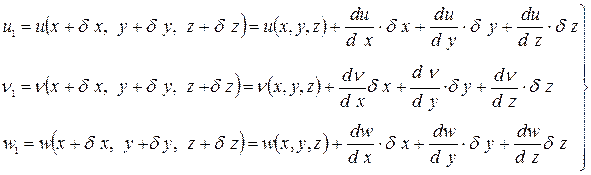(4)

Совершим следующую тождественную замену выражений производных в правых частях системы (4):

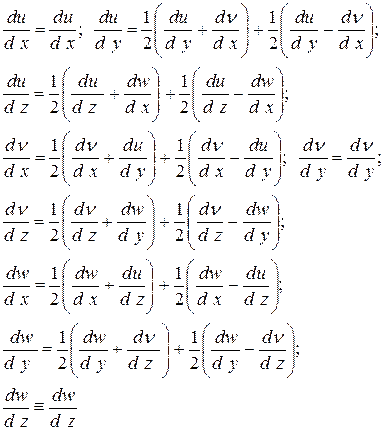
С учётом этого выражения (4) примут вид:

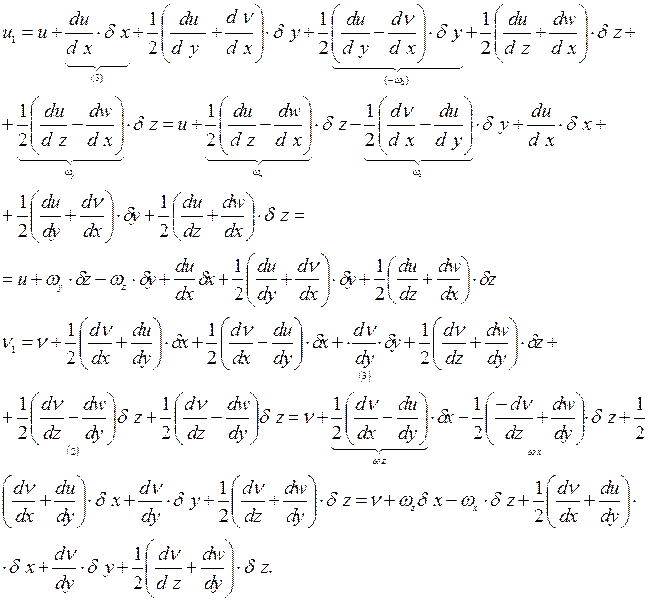
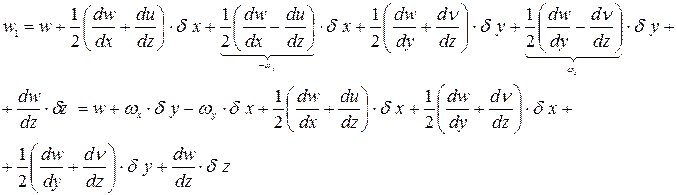
Если сравнить 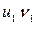и 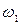с выражениями для 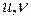и 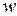(2), то мы видим, что первые три слагаемых в правых частях, описывающих движение недеформируемого объёма совпадают, а оставшиеся слагаемые описывают деформационную составляющую движения сплошной среды.

Ввёдём следующие обозначения:

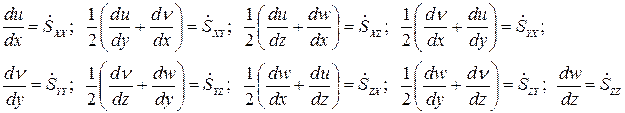
Совокупность девяти величин (различных среди них только 6: 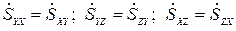)образуют тензор :

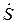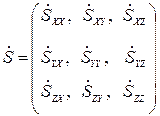- именуемый тензором скоростей деформаций.

Этот тензор симметричен, его компоненты, зеркально расположенные относительно главной диагонали, равны между собой.

С учётом новых обозначений

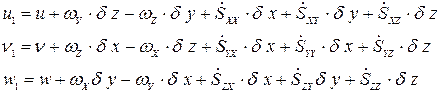
В векторной форме эти выражения перепишутся в следующем виде:

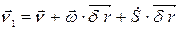- Первая теорема Гельмгольца: движение элементарного объёма сплошной среды можно в каждый данный момент времени представить себе разложенным на:

1. «Квазитвёрдое» движение со скоростью равной сумме поступательного движения 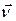,какой - нибудь отдельной частицы 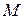, заключённой в этом элементарном объёме, и вращательной 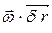вокруг точки .

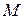2. «Деформационное» движение, определяемое тензором скоростей деформации.