2014-09-04
1056
Как и для несжимаемой жидкости, газ представляет «ньютоновскую» среду, подчинённую известному обобщённому закону Ньютона о линейной связи между тензором напряжений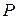 
и тензором скоростей деформаций 
.
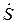В отличие от несжимаемой жидкости, в случае газа, который будем считать, так же средой изотропной формула обобщённого закона Ньютона примет вид:
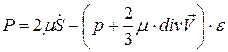(10)
Или в матричной форме:
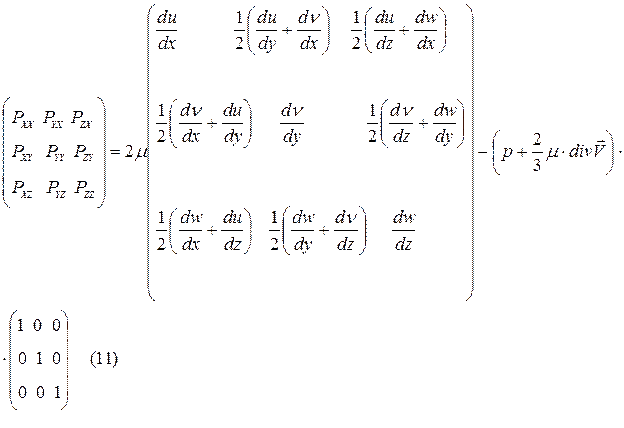
Для вывода уравнений динамики вязкого газа используем уравнение в напряжениях, что при выводе уравнений Стокса:
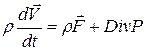(12)
Или подставляем 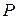из(10) получим:
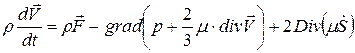
Проведя все операции преобразования как для уравнений Стокса (несжимаемой изотермической жидкости) получим уравнения Навье – Стокса для сжимаемого неизотермического вязкого газа. В проекциях на оси координат получим:
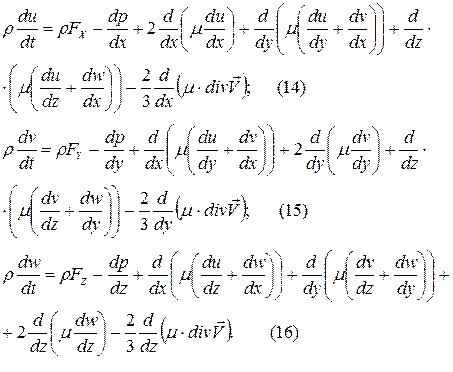
При решении задачи течения газа к этим уравнениям добавляется уравнение неразрывности:
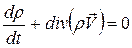(17)
Формула Саттерленда для вычисления коэффициента вязкости:
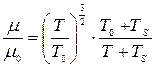(18)
(
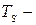постоянная Саттерленда, известна из таблиц для всех газов)
Уравнение состояния газа, в предположении, что газ совершенен, т.е. давление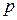 
, плотность 
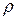и температура газа 
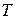удовлетворяют уравнению Клайперона:
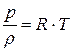(19)
Наличие неизотермического течения газа (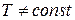
) делает систему уравнений 
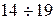незамкнутой. Число неизвестных 
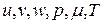- семь, а уравнений 6.
Чтобы получить замкнутую систему уравнений, составим ещё уравнение баланса тепла в движущемся газе. С этой целью используем уравнение баланса энергии в дифференциальной форме:
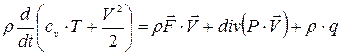(20)
Вспомним, что энтальпия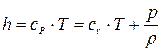 
(где 
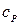и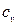 
- удельные теплоёмкости газа при постоянном давлении и объёма – константы не зависят от Т и следовательно 
)
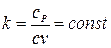Кроме того, будем считать, что приток тепла имеет место только через теплопроводность:
,
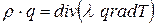Где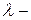 
коэффициент теплопроводности является функцией температуры 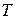и пропорционален 
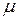, т.е. число Прандтля 
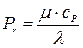рассматривается как физическая константа газа.
Кроме этого заменяя в выражении (20) тензор напряжения 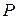его выражением (10) получим:
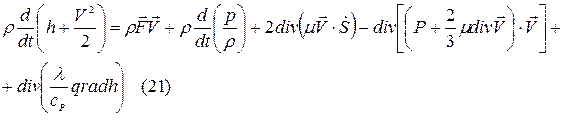
Рассмотрим отдельно:
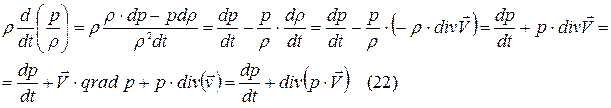Т.к. 
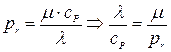(23)
С учётом (23) и (22) уравнение (21) примет вид:
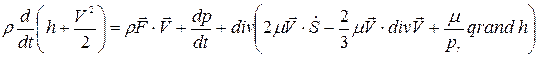(24)
Добавляя это уравнение баланса тепла мы замыкаем систему уравнений
