§ 1. Распределение массы в сплошной среде.
Возьмём малый объём жидкости или газа 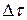 , содержащий внутри себя некоторую точку
, содержащий внутри себя некоторую точку 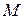 пространства. Пусть масса этого объёма будет
пространства. Пусть масса этого объёма будет 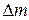 .Скалярная величина
.Скалярная величина 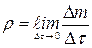 причём предполагается, что при стремлении объёма
причём предполагается, что при стремлении объёма 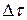 к нулю точка
к нулю точка 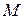 всё время остаётся внутри объёма
всё время остаётся внутри объёма 

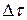 , называется плотностью распределения массы или, короче, плотностью среды в данной точке
, называется плотностью распределения массы или, короче, плотностью среды в данной точке 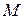 . Обратную величину
. Обратную величину 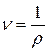 -называют удельным объёмом. Размерность плотности в системе СИ
-называют удельным объёмом. Размерность плотности в системе СИ 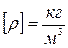 , удельного объёма
, удельного объёма 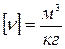 .
.
Плотность движущейся среды зависит от её материального состава, от температуры, давления и характера движения среды. В общем случае плотность скалярная функция координат и времени:
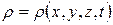
и образует скалярное поле, которое может быть как стационарным, так и нестационарным.
Поверхности или в частном случае линии равных плотностей сплошной среды называются изостерическими поверхностями или линиями, короче, изостерами.
Плотность жидкости (вода, бензин и др.) слабо зависит от температуры и почти не зависит от давления, так как под влиянием даже больших давлений объём жидкости меняется сравнительно мало. Так, например, относительное изменение объёма воды при увеличении давления на 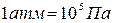 и сохранении температуры чуть меньше 0, 00005, глицерина – 0,000025, керосина – 0,000077 и т. д.
и сохранении температуры чуть меньше 0, 00005, глицерина – 0,000025, керосина – 0,000077 и т. д.
Наоборот, плотность газов сильно меняется с давлением и температурой. Напомним, что по закону Бойля – Мариотта (изотермический процесс 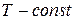 ) плотность газа прямо пропорциональна давлению, а по закону Гей – Люсака (изобарический процесс
) плотность газа прямо пропорциональна давлению, а по закону Гей – Люсака (изобарический процесс  ) плотность газа растёт обратно пропорционально его абсолютной температуре.
) плотность газа растёт обратно пропорционально его абсолютной температуре.
Таблицы плотностей и газов можно найти в различных «нормальных» условиях.(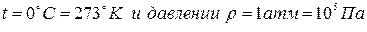 ).
).
Исходя из справедливого для классической механики закона сохранения массы индивидуального объёма сплошной среды, для любой элементарной массы 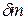 , имеющей объём
, имеющей объём 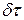 , будем иметь:
, будем иметь:
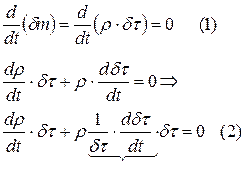
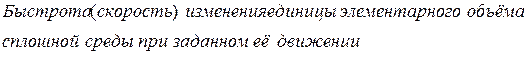
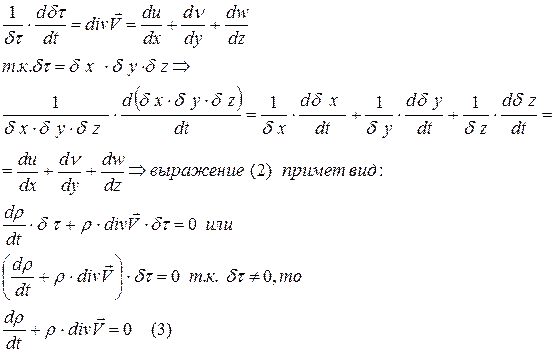
Уравнение(3) называется уравнением неразрывности.
Т.к. 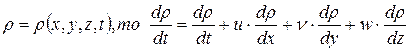
Тогда выражение (3) перепишется в виде:
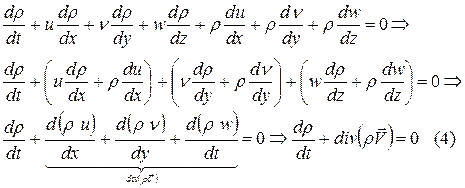
В случае стационарного поля плотности 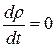 и уравнение неразрывности упрощается:
и уравнение неразрывности упрощается:
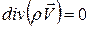 (5)
(5)
Если жидкость несжимаема 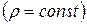 , то уравнение неразрывности переходит в уравнение несжимаемости:
, то уравнение неразрывности переходит в уравнение несжимаемости:
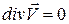 (6)
(6)
 2014-09-04
2014-09-04 1122
1122
