2014-09-04
1730
В кинематике используется только одно свойство, общее для всех жидкостей и газов и присущее всякой сплошной среде; это – непрерывность распределение кинематических элементов в пространстве и дифференцируемость их в пространстве и времени; всё, что мы изучаем в этой главе, применимо для любой сплошной среды.
В теоретической механике мы изучали механику или отдельной материальной точки или системы материальных точек. Механика сплошной среды имеет свои специфические для неё приёмы задания движения.
Пусть некоторая частица среды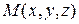 
в момент времени 
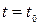занимала положение 
;
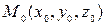её координаты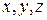 
являются функциями:
1. Времени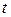 
;
2. Начальными координатами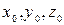 
Т.е.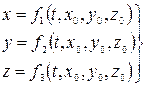 
Зная эти функции не трудно построить уравнение траектории движения этой частицы среды (вспоминаем теоретическую механику – координатный способ задания движения точки), определить её вектор скорости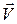 
и ускорения 
.
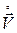Проекции вектора скорости 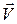и ускорения 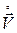на оси координат 
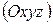соответственно будут:
на ось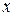 
: 
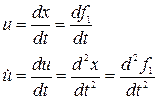
на ось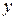 
: 
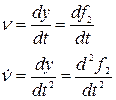
на ось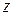 
: 
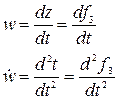
Такой метод описания движения сплошной среды как движение отдельных частиц носит название Лагранжа, а переменные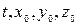 
- называются переменными Лагранжа.
Другой метод описания движения сплошной среды, предложен и соответственно называемый методом Эйлера, заключается в выражении скоростей частиц среды в функции от времени 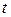, и координат 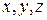точек пространства, по отношению к которому происходит Движение жидкости, т. е. задание поля скоростей. Совокупность 
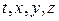называют переменными Эйлера, Движение среды, по Эйлеру, задаётся полем скоростей:
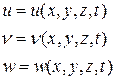
Основное отличие методов Лагранжа и Эйлера заключается в том, что в методе Лагранжа величины 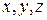- переменные координаты движущейся частицы жидкости, а в методе Эйлера – это координаты фиксированных точек пространства, мимо которых (через которые) в данный момент времени проходят различные частицы сплошной среды.
