Равномерное движение материальной точки по окружности

Пусть материальная точка движется с постоянной по модулю скоростью v по окружности радиуса R. При таком движении направление вектора скорости v постоянно изменяется (рис. 71), следовательно, как и при любом криволинейном движении, движение по окружности есть движение с ускорением.

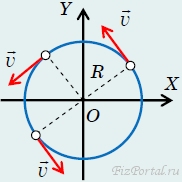
рис. 71

Рассмотрим изменение вектора скорости тела за малый промежуток времени  Δt (рис. 72). Обозначим положение точки, движущейся по окружности радиуса R, в некоторый момент времени А_o.

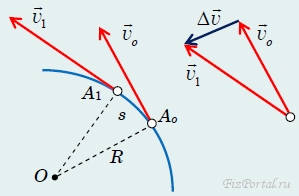
рис. 72

Вектор скорости  v_o в этот момент направлен по касательной к окружности, то есть перпендикулярно радиусу ОА_o. За время Δt частица переместилась в точку A₁, ее скорость v₁ изменила направление и стала перпендикулярна радиусу ОА₁ (но модуль ее остался неизменным: |v_o| = |v₁| = v). Для того чтобы вычислить изменение скорости, совместим начало векторов v_o и v₁. Тогда треугольник, образованный векторами скоростей, подобен треугольнику OA_oA₁. Из подобия этих треугольников следует

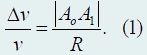
Если рассматривать изменение положения частицы и ее скорости за очень малый промежуток времени, то длина хорды  |А_oА₁| будет очень близка к длине дуги А_oА₁

S = vΔt,

поэтому

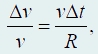
откуда получаем

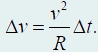
Таким образом, модуль ускорения точки равен:

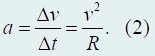
Чтобы полностью определить вектор ускорения, необходимо выяснить его направление. Заметим, что при малой величине  Δt угол между векторами v_o и v₁ крайне мал, поэтому можно считать, что вектор изменения скорости направлен перпендикулярно¹ как вектору v_o, так и вектору v₁. Следовательно, вектор ускорения в данном случае направлен к центру окружности.
Вектор ускорения точки при ее равномерном движении по окружности направлен к центру окружности, а его модуль равен  v²/R. Такое ускорение называется центростремительным.
Как мы уже отмечали ранее, материальная точка, движущаяся по заданной линии, обладает одной степенью свободы, поэтому ее положение однозначно определяется одной координатой. В случае движения точки по окружности в качестве такой единственной координаты удобно выбрать угол поворота. 

Пусть материальная точка движется по окружности радиуса R. Введем декартовую систему координат, начало которой совместим с центром окружности (рис. 74). Положение точки на окружности однозначно определяется углом φ между осью X и радиус-вектором точки.

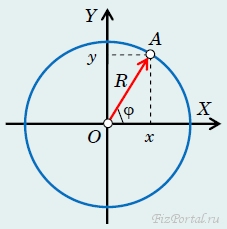
рис. 74

Конечно, оси координат можно направить произвольно, да и угол можно отсчитывать от оси  Y, однако мы в дальнейшем для однозначности будем отсчитывать угол поворота от оси X в направлении против часовой стрелки.
Декартовые координаты точки однозначно выражаются через угол поворота по формулам 

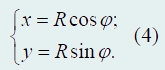
При движении точки ее координата, то есть угол поворота, изменяется, становится функцией времени. Поэтому закон движения в этом случае представляется функцией  φ(t), то есть зависимости угла поворота от времени.
По аналогии с одномерным движением введем понятие угловой скорости. 
Угловой скоростью  ω называется отношение угла поворота к промежутку времени, в течение которого этот поворот произошел, при промежутке времени, стремящемся к нулю:

Единицей угловой скорости является рад/с − радиан в секунду, однако так как радиан является безразмерной величиной, размерность угловой скорости может быть просто  1/с = с⁻¹ − секунда в минус первой степени.
При равномерном движении по окружности угловая скорость является постоянной и равна углу поворота в единицу времени. Время одного оборота (эту величину еще называют период вращения)  Т легко найти, если вспомнить, что один оборот соответствует углу поворота 2π, поэтому

T = 2π/ω. (6)

Число оборотов в единицу времени называют частотой вращения, и она вычисляется по формуле

n = 1/T = ω/(2π). (7)

Установим связь между угловой и линейной скоростями при движении материальной точки по окружности. Модуль линейной скорости определяется как отношение пройденного пути к промежутку времени, за который этот путь пройден  v = S/Δt, а при движении по окружности длина пути (длина дуги окружности) выражается через угол поворота (выраженный в радианах): s = RΔφ, поэтому

v = RΔφ/Δt = Rω. (8)

Запишем также выражение для центростремительного ускорения, используя понятие угловой скорости: 

a = v²/R = (Rω)²/R = Rω². (9)

Специально отметим, что формулы (8) и (9) остаются справедливыми при движении по окружности и в том случае, когда скорость точки изменяется по абсолютной величине. Так, при выводе формулы (8) можно рассмотреть случай Δt → 0. В таком пределе скорость v будет являться мгновенной скоростью, а ω − мгновенной угловой скоростью.

При вращении вокруг фиксированной оси направление вращения может иметь только два значения − по часовой стрелке и против часовой стрелки. Поэтому в этом случае можно говорить о двух знаках угловой скорости, обычно − плюс при вращении против часовой стрелки и минус − при вращении по часовой стрелке. Для того чтобы описать произвольное вращение, необходимо задать также ось вращения. Оказывается, удобно задавать ось вращения с помощью вектора, направленного вдоль этой оси. Если совместить эти две характеристики вращения, то получим вектор угловой скорости  ω, направление которого совпадает с осью вращения, а модуль равен определенной нами угловой скорости. Используя математическую операцию векторного произведения, можно записать выражение для связи между линейной и угловой скоростями:

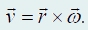
Аналогично можно определить вектор углового ускорения: 

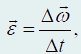
который определяет не только изменение скорости вращения, но и изменение оси вращения.