Скорость точки

Способы задания движения точки.

Задать движение точки – это значит указать правило, по которому в любой момент времени можно определить её положение в заданной системе отсчёта.

Математическое выражение этого правила называется законом движения, или уравнением движения точки.

Существует три способа задания движения точки:

векторный;

координатный;

естественный.

Чтобы задать движение векторным способом, нужно:

à выбрать неподвижный центр;

à положение точки определить с помощью радиус-вектора , начинающегося в неподвижном центре и заканчивающемся в движущейся точке М;

à определить этот радиус-вектор как функцию от времени t: .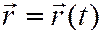

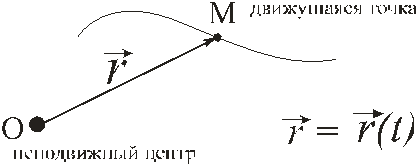
Выражение

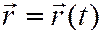
называется векторным законом движения точки, или векторным уравнением движения.

!! Радиус-вектор – это расстояние (модуль вектора) + направление от центра О на точку М, которое можно определять разными способами, например, углами с заданными направлениями.

Чтобы задать движение координатным способом, нужно:

à выбрать и зафиксировать систему координат (любую: декартову, полярную, сферическую, цилиндрическую и проч.);

à определить положение точки с помощью соответствующих координат;

à задать эти координаты, как функции от времени t.

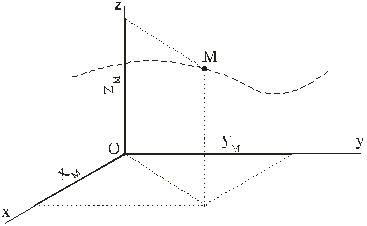
В декартовой системе координат, таким образом, надо указать функции

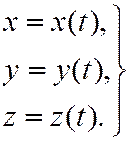
В полярной системе координат следует определить как функции от времени полярный радиус и полярный угол:

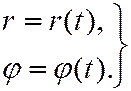
В общем, при координатном способе задания следует задавать как функции от времени те координаты, с помощью которых определяется текущее положение точки.

Чтобы можно было задавать движение точки естественным способом, нужно знать её траекторию. Запишем определение траектории точки.

Траекторией точки называется множество её положений за какой-либо промежуток времени (обычно – от 0 до +¥).

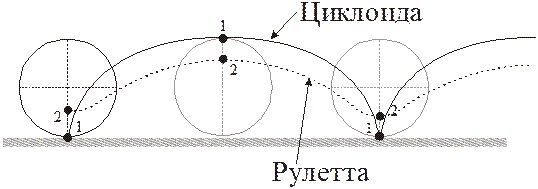
В примере с катящимся по дороге колесом траекторией точки 1 является циклоида, а точки 2 – рулетта; в системе отсчёта, связанной с центром колеса, траектории обеих точек – окружности.

Чтобы задать движение точки естественным способом, нужно:

à знать траекторию точки;

à на траектории выбрать начало отсчёта и положительное направление;

à определить текущее положение точки длиной дуги траектории от начала отсчёта до этого текущего положения;

à указать эту длину как функцию от времени.

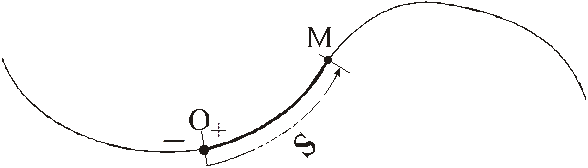
Выражение, определяющее указанную выше функцию,

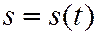
называют законом движения точки по траектории, или естественным уравнением движения точки.

В зависимости от вида функции (4) точка по траектории может двигаться различным образом.

3. Траектория точки и её определение.

Определение понятия «траектория точки» был дано ранее в вопросе 2. Рассмотрим вопрос об определении траектории точки при разных способах задания движения.

Естественный способ: траектория должна быть задана, так что находить её не надо.

Векторный способ: нужно перейти к координатному способу согласно равенствам

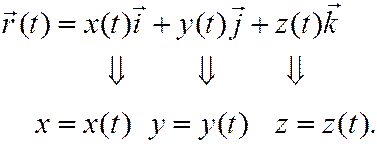
Координатный способ: нужно из уравнений движения (2), или (3) исключить время t.

Координатные уравнения движения задают траекторию параметрически, через параметр t (время). Для получения явного уравнения кривой надо параметр исключить из уравнений.

После исключения времени из уравнений (2) получаются два уравнения цилиндрических поверхностей, например, в виде

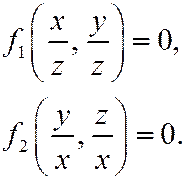
Пересечение этих поверхностей и будет траекторией точки.

При движении точки по плоскости задача упрощается: после исключения времени из двух уравнений

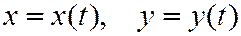
уравнение траектории получится в одной из следующих форм:

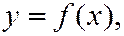
или

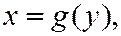
или

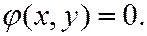
ПРИМЕРЫ.

1)

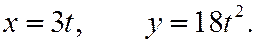
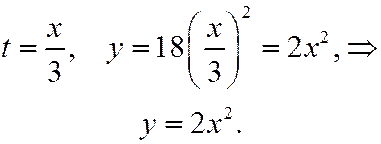
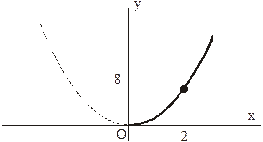
При 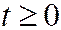будет 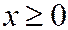, поэтому траекторией точки будет правая ветвь параболы:

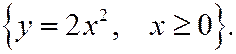
2)

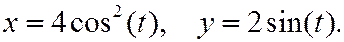
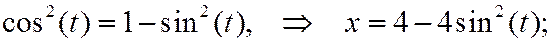
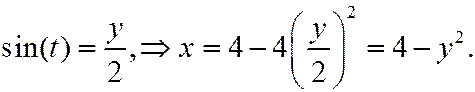
Из уравнений движения следует, что

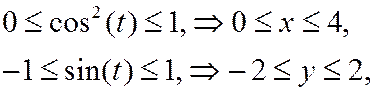
поэтому траекторией точки будет часть параболы, расположенная в правой полуплоскости:

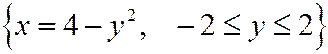
3) 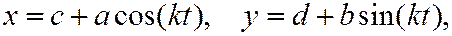где

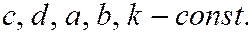
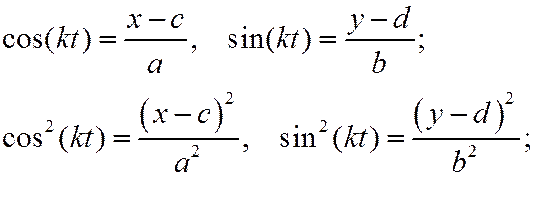
Тогда получим

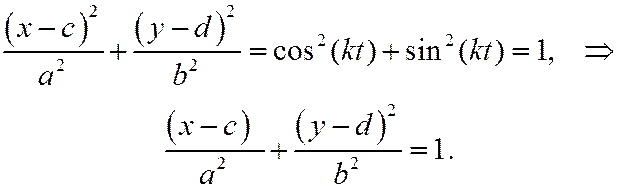
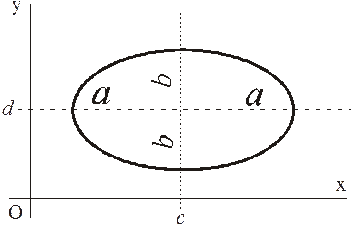
Так как 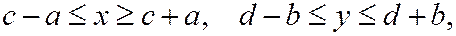то весь эллипс будет траекторией точки.

При 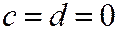центр эллипса будет в начале координат О; при 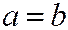получим окружность; параметр k на форму эллипса не влияет, от него зависит скорость движения точки по эллипсу. Если в уравнениях поменять местами cos и sin, то траектория не изменится (тот же эллипс), но изменится начальное положение точки и направление движения.

Скорость точки характеризует «быстроту» изменения её положения. Формально: скорость – перемещение точки за единицу времени.

Точное определение.

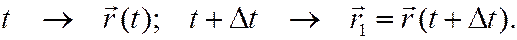
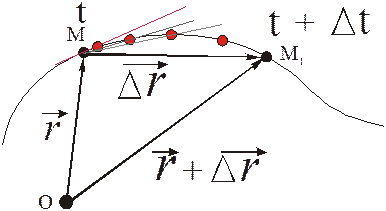
Тогда 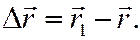Отношение

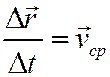
называется средней скоростью за промежуток времени Dt.

Переходя в (9) к пределу при 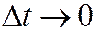получим

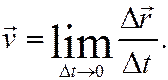
получим мгновенную скорость точки, или скорость точки в данный момент, или скорость точки.

Так как

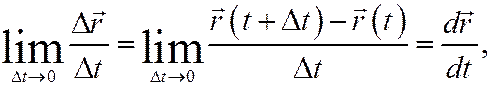
то, окончательно,

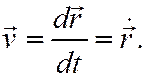
Видно, что при 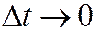секущая, по которой направлен вектор 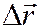, стремится к касательной к траектории точки. Следовательно,

вектор скорости точки всегда направлен по касательной к её траектории.

При координатном способе задания движения в декартовой системе координат вектор скорости определяется по проекциям на оси координат:

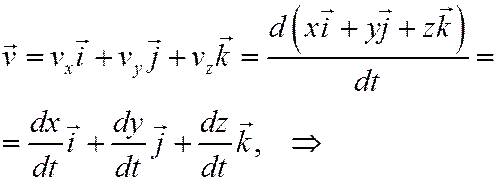
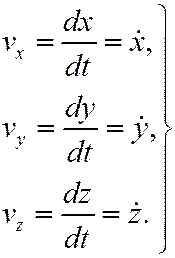
Модуль (величина) скорости

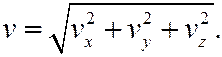
При естественном способе задания движения будет

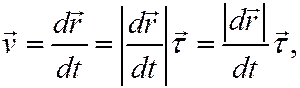
где 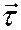– единичный вектор касательной, а

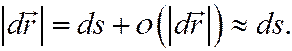
В этом равенстве 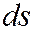– приращение длины дуги траектории точки.

Тогда, окончательно,

Выражение

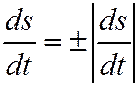
–это проекция вектора скорости на касательную, а

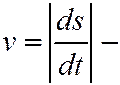
это модуль (величина) скорости.