Волновая функция 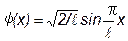 описывает основное состояние частицы в бесконечно глубоком прямоугольном ящике шириной l. Вычислить вероятность нахождения частицы в малом интервале Dl =0,01l в двух случаях: 1) вблизи стенки (0 £ х £Dl); 2) в средней части ящика
описывает основное состояние частицы в бесконечно глубоком прямоугольном ящике шириной l. Вычислить вероятность нахождения частицы в малом интервале Dl =0,01l в двух случаях: 1) вблизи стенки (0 £ х £Dl); 2) в средней части ящика 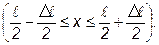
 |
Дано: Решение

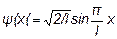
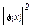
Dl =0,01l
0 £ х £Dl 2/l
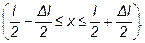
 w1, w2 -? x
w1, w2 -? x
Dℓ Dℓ
Рис.27
Вероятность того, что частица будет обнаружена в интервале dx (от x до x+ dx), пропорциональна этому интервалу и квадрату модуля волновой функции, описывающей данное состояние, равна
dw = |y(x)| 2 dx.
В первом случае искомая вероятность найдется интегрирование в пределах от 0 до 0,01l ( рис.27):
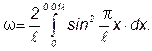 (1)
(1)
Знак модуля опущен, так как y - функция в данном случае не является комплексной.
Так как х изменяется в интервале 0£ х£ 0,01l и, следовательно 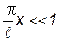 , справедливо приближенное равенство
, справедливо приближенное равенство
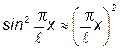 .
.
С учетом этого выражение (1) примет вид
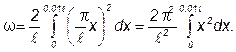
После интегрирования получим:
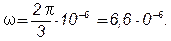
Во втором случае можно обойтись без интегрирования, так как квадрат модуля волновой функции вблизи ее максимума в заданном малом интервале (Dl = 0,001l) практически не изменяется. Искомая вероятность во втором случае определяется выражением
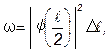
или
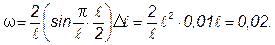
 2015-01-21
2015-01-21 395
395








