На группу действуют известные внешние силы: силы тяжести звеньев 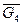 и
и 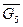 , силы инерции
, силы инерции 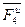 и
и 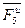 , момент сил инерции
, момент сил инерции 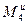 и сила полезного сопротивления
и сила полезного сопротивления  (рис. 6).
(рис. 6).
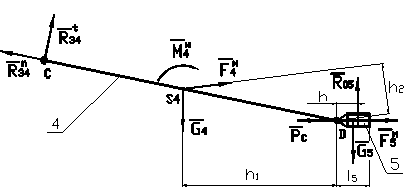
Рис. 6. Группа Асура 4-5.
При выделении из механизма группы Ассура или отдельного звена необходимо действие отсоединённой части механизма заменить реакциями связи, приложенными к соответствующим элементам кинематических пар. Условимся силу, действующую на звено i со стороны звена k, обозначать через 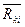 . Требуется найти силы взаимодействия звеньев 4 и 5 между собой, т. е. реакцию
. Требуется найти силы взаимодействия звеньев 4 и 5 между собой, т. е. реакцию 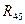 либо
либо 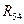 в шарнире D, силу со стороны отсоединенного звена 3механизма на звено 4, т. е. реакцию
в шарнире D, силу со стороны отсоединенного звена 3механизма на звено 4, т. е. реакцию 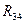 в шарнире С; реакции опоры звена 5, т.е. реакцию
в шарнире С; реакции опоры звена 5, т.е. реакцию 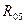 .
.
Реакция 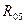 направлена перпендикулярно направляющим ползуна и приложена на расстоянии h от шарнира D. Направление реакции
направлена перпендикулярно направляющим ползуна и приложена на расстоянии h от шарнира D. Направление реакции 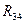 неизвестно, поэтому реакцию
неизвестно, поэтому реакцию 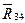 раскладываем на нормальную составляющую
раскладываем на нормальную составляющую 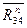 , направленную вдоль звена CD, и тангенциальную составляющую
, направленную вдоль звена CD, и тангенциальную составляющую  , направленную перпендикулярно звену CD.
, направленную перпендикулярно звену CD.
Прикладываем неизвестные реакции 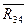 и
и 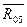 и составляем систему уравнений равновесия исследуемой группы Асура:
и составляем систему уравнений равновесия исследуемой группы Асура:
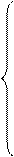
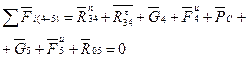 (3)
(3)
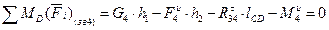 (4)
(4)
 (5)
(5)
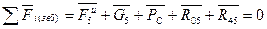 (6)
(6)
Величину  можно получить из уравнения равновесия составленного для звена 4 относительно шарнира D (4).
можно получить из уравнения равновесия составленного для звена 4 относительно шарнира D (4).
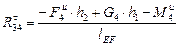 (7)
(7)
Замечание: Так как направление составляющей 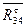 пока неизвестно, то при составлении уравнения моментов задаемся произвольным направлением ее. Если после определения величина этой составляющей окажется отрицательной, то ее истинное направление будет противоположно выбранному.
пока неизвестно, то при составлении уравнения моментов задаемся произвольным направлением ее. Если после определения величина этой составляющей окажется отрицательной, то ее истинное направление будет противоположно выбранному.
В уравнении (3) известны: величина, направление, точка приложения сил 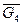 ,
, 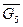 ,
, 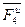 ,
, 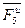 ,
,  и
и 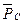 а также линии действия реакций
а также линии действия реакций 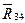 и
и 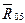 .
.
Теперь в это векторное уравнение входят только два неизвестных скаляра — величина составляющей 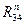 , направленной по оси CD звена 4 и величина реакции
, направленной по оси CD звена 4 и величина реакции 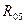 , направленной перпендикулярно направляющей опоре. Поэтому задачу можно решить графически методом построения плана сил. Для этого из любой точки а плоскости (рис.7) откладываем в произвольном масштабе
, направленной перпендикулярно направляющей опоре. Поэтому задачу можно решить графически методом построения плана сил. Для этого из любой точки а плоскости (рис.7) откладываем в произвольном масштабе 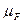 составляющую
составляющую 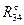 реакции
реакции 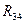 в виде вектора
в виде вектора 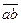 . К вектору
. К вектору 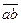 геометрически прибавляем вектор
геометрически прибавляем вектор 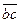 , изображающий в том же масштабе
, изображающий в том же масштабе 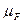 силу
силу 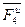 .
.
Масштаб определяется по формуле:


Рис. 7. Силовой многоугольник для группы Асура 4-5.
Продолжая далее геометрическое сложение в порядке, указанном в уравнении (3), получаем последовательно вектор 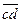 изображающий силу
изображающий силу  , вектор
, вектор 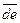 , изображающий силу
, изображающий силу 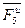 , вектор
, вектор 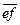 , изображающий силу
, изображающий силу 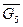 и вектор
и вектор 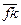 , изображающий силу
, изображающий силу 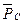 . Далее через начало а вектора
. Далее через начало а вектора 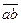 проводим прямую в направлении действия второй составляющей
проводим прямую в направлении действия второй составляющей 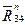 реакции
реакции 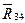 , т.е. параллельно оси CD звена 4, а через конечную точку k вектора
, т.е. параллельно оси CD звена 4, а через конечную точку k вектора 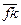 прямую в направлении действия реакции
прямую в направлении действия реакции 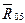 , т. е. перпендикулярно направляющей опоре. Точка l пересечения этих прямых определяет начало вектора
, т. е. перпендикулярно направляющей опоре. Точка l пересечения этих прямых определяет начало вектора  составляющей
составляющей 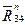 и конечную точку вектора
и конечную точку вектора  составляющей
составляющей 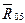 . Полную реакцию
. Полную реакцию 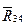 можно получить сложив графически её составляющие
можно получить сложив графически её составляющие 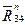 и
и 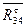 . Соединив точку l с точкой b, получим реакцию
. Соединив точку l с точкой b, получим реакцию 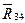 в виде вектора
в виде вектора  .
.
Величину неизвестных реакций (например 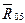 ) находим следующим образом:
) находим следующим образом:
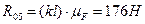
Из уравнения (5) найдём точку приложения реакции 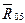 , находящейся на расстоянии h от шарнира D:
, находящейся на расстоянии h от шарнира D:
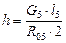 (8)
(8)
Для определения реакции  звена 4 на звено 5 воспользуемся уравнением равновесия сил, действующих на звено 5 в векторном виде (6), вычертив соответствующий силовой многоугольник.
звена 4 на звено 5 воспользуемся уравнением равновесия сил, действующих на звено 5 в векторном виде (6), вычертив соответствующий силовой многоугольник.
Замечание: Для решения полученного векторного уравнения можно воспользоваться силовым многоугольником, построенным ранее (рис.7). Если мы вначале сложили только все силы, действующие на звено 4, то достаточно соединить точки d и l. В результате получим реакцию  в виде вектора
в виде вектора 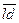 (рис.8).
(рис.8).

Рис. 8. Определение реакции в кинематической паре D.
Замечание: На плане сил вектор 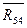 представлен тем же отрезком, что и вектор
представлен тем же отрезком, что и вектор  , но имеет противоположное направление.
, но имеет противоположное направление.
Определив реакции в группе ВВП, переходим к следующей группе Асура (рис.5) – двухповодковой группе с тремя вращательными кинематическими парами (ВВВ).
 2014-09-04
2014-09-04 1876
1876








