2015-01-21
822
ЭСМ включает структурную математическую формулировку задачи (Эволюционно-симулятивная модель) и алгоритмы поиска ее решения. Этот метод отражает процессы формирования:
· равновесия на товарных, финансовых и фондовых рынках;
· процессы управления, основанные на нормативах;
· физические, биологические и химические равновесные процессы.
К ЭСМ сводятся некоторые задачи стохастического программирования, байесовский подход, статистическая оптимизация. Название получено путем объединения двух терминов: «Эволюционный» и «Симулятивный». Эволюционный — потому, что в ЭСМ применен алгоритм оптимизации, моделирующий законы естественной эволюции, представляющие собою направленный случайный поиск. Симулятивный — потому, что в ЭСМ использованы принципы диалогового (симулятивного) моделирования с применением экспертных оценок.
Первая публикация об ЭСМ была в 1970 году. На основе ЭСМ создана инструментальная система Decision. На основании Решения Международной Ассоциации Авторов Научных Открытий, членами которой являются 28 Лауреатов Нобелевской Премии, Президиум Российской Академии Естественных Наук признал Decision открытием (решение № 126 от 15.06.2000).
38. Основные теоремы двойственности и их экономическое содержание
Каждой задаче линейного программирования можно поставить в соответствие другую задачу линейного программирования, которую называют двойственной к данной. Исходная и двойственная к ней задача образуют пару двойственных задач. В зависимости от вида исходной задачи линейного программирования различают симметричные, несимметричные и смешанные пары двойственных задач.
Симметричные пары двойственных задач - Если система ограничений исходной задачи состоит из неравенств и на все переменные хj наложено условие неотрицательности, то исходная задача и составленная по определенному правилу двойственная задача образуют симметричную пару двойственных задач.
Лемма 1. Есл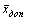и 
и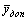 
- произвольные допустимые решения пары двойственных задач, то 
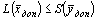, если исходная задача на максимум, и 
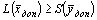, если она на минимум. Лемма 2. Достаточный признак оптимальности.
Есл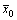и 
и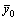 
- допустимые решения пары двойственных задач, для которых выполняется равенство 
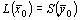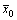, то и 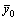- оптимальные решения соответствующих задач.
Теорема 1. (Первая основная теорема двойственности.) Если одна из двойственных задач имеет оптимальное решение, то двойственная ей задача также имеет оптимальное решение, причем экстремумы целевых функций равны, т.е.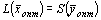 
.
Если одна из двойственных задач не имеет оптимального решения, то другая задача также не имеет оптимального решения, причем если одна из задач не имеет оптимального решения из-за неограниченности целевой функции, то другая из-за несовместности системы ограничений.
Теорема 2. (Вторая основная теорема двойственности.) Для того чтобы допустимые решения 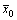и 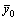несимметричной пары двойственных задач были соответственно оптимальными решениями, необходимо и достаточно, чтобы для любого j выполнялось равенство 
.
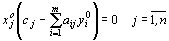Эк интерпретация: основные переменные хi обозначали количество произведенной продукции i-го вида, дополнительные переменные обозначали количество излишков соответствующего вида ресурсов, каждое из неравенств выражало собой расход определенного вида сырья в сравнении с запасом этого сырья. Целевая функция определяла прибыль при реализации всей продукции. Предположим теперь, что предприятие имеет возможность реализовывать сырье на сторону. Какую минимальную цену надо установить за единицу каждого вида сырья при условии, чтобы доход от реализации всех его запасов был не меньше дохода от реализации продукции, которая может быть выпущена из этого сырья. Переменные у1, у2, у3 будут обозначать условную предполагаемую цену за ресурс 1, 2, 3 вида соответственно.
39. Основные теоремы теории равновесных случайных процессов
Це́пь Ма́ркoва — последовательность случайных событий с конечным или счётным числом исходов, характеризующаяся тем свойством, что, говоря нестрого, при фиксированном настоящем будущее независимо от прошлого. Названа в честь А. А. Маркова (старшего).
Определение Последовательность дискретных случайных величин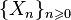 
называется простой цепью Маркова (с дискретным временем), если
.
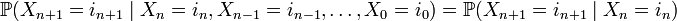Таким образом, в простейшем случае условное распределение последующего состояния цепи Маркова зависит только от текущего состояния и не зависит от всех предыдущих состояний (в отличие от цепей Маркова высших порядков).
Область значений случайных величин 
называется простра́нством состоя́ний цепи, а номер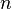 
— номером шага.
ВИНЕРА-ХИНЧИНА ТЕОРЕМА -утверждение о том, что спектральная плотность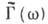 
стационарного случайного процесса 
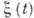, связанная с его корреляц. ф-цией 
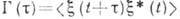преобразованием Фурье:
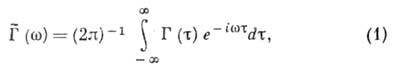
неотрицательна,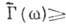 
О (угловые скобки означают статистич. усреднение, * - комплексное сопряжение). Спектральную плотность наз. также спектром мощности случайного процесса. В.-X. т. получена H. Винером (N. Wiener) в 1930, в иной формулировке - А. Я. Хинчиным в 1934.
40. Особые случаи симплексного метода.
Существуют следующие четыре особых случая, встречающихся при использовании симплекс-метода:
1. Вырожденность. В ходе выполнения симплекс-метода проверка условия допустимости может привести к неоднозначному выбору исключаемой переменной. В этом случае на следующей итерации одна или более базисных переменных примут нулевое значение. Тогда новое решение будет вырожденным.
В вырожденном решении нет никакой опасности, за исключением небольших теоретических неудобств, которые мы далее кратко обсудим. С практической точки зрения вырожденность объясняется тем, что в исходной задаче присутствует, по крайней мере, одно избыточное ограничение.
2. Альтернативные оптимальные решения. Когда прямая (если рассматривается двухмерная задача ЛП, в общем случае – гиперплоскость), представляющая целевую функцию, параллельна прямой (гиперплоскости), соответствующей связывающему неравенству (которое в точке оптимума выполняется как точное равенство), целевая функция принимает одно и то же оптимальное значение на некотором множестве точек границы области допустимых решений. Эти решения называются альтернативными оптимальными решениями.
На практике альтернативные оптимальные решения весьма полезны, поскольку позволяют сделать выбор среди множества решений без ухудшения значения целевой функции.
3. Неограниченные решения. В некоторых задачах ЛП значения переменных могут неограниченно возрастать без нарушения ограничений. Это говорит о том, что пространство допустимых решений не ограничено, по крайней мере, по одному направлению. В результате этого целевая функция может возрастать (задача максимизации) или убывать (задача минимизации) неограниченно.
Неограниченность решения задачи свидетельствует только об одном: модель разработана не достаточно корректно. Типичные ошибки, приводящие к построению таких моделей, заключается в том, что не учитываются ограничения, не являющиеся избыточными, и не точно оцениваются параметры (коэффициенты) ограничений.
Правило выявления неограниченности решения следующее. Если на какой-либо симплекс-итерации коэффициенты в ограничениях для какой-нибудь небазисной переменной будут неположительными, значит, пространство решений не ограничено в направлении возрастания этой переменной. Кроме того, если коэффициент этой переменной в z-строке отрицателен, когда рассматривается задача максимизации, или положителен в задаче минимизации, целевая функция также не ограничена
4. Отсутствие допустимых решений. Если ограничения задачи ЛП несовместны (т.е. они не могут выполняться одновременно), то задача не имеет допустимых решений. Такая ситуация не может возникнуть, если все неравенства, составляющие систему ограничений, имеют тип «<=» с неотрицательными правыми частями, так как в этом случае дополнительные переменные могут составить допустимое решение. Для других типов ограничений мы используем искусственные переменные. И хотя в оптимальном решении все искусственные переменные в силу штрафов равны нулю, такой исход возможен только тогда, когда задача имеет непустое пространство допустимых решений. В противном случае, в оптимальном решении будет присутствовать хотя бы одна положительная искусственная переменная.
С практической точки зрения отсутствие допустимых решений свидетельствует о том, что задача плохо сформулирована.
41. Оценка параметров линейной модели парной регрессии. Суть метода наименьших квадратов.
Линейная регрессия находит широкое применение в эконометрике ввиду четкой экономической интерпретации ее параметров. Линейная регрессия сводится к нахождению уравнения вида: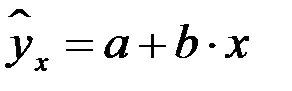 
или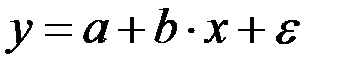 
. Уравнение вида 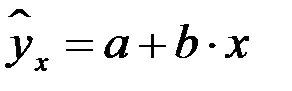позволяет по заданным значениям фактора 
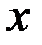находить теоретические значения результативного признака, подставляя в него фактические значения фактора 
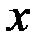. Построение линейной регрессии сводится к оценке ее параметров – 
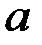и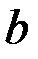 
. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров 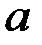и 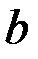, при которых сумма квадратов отклонений фактических значений результативного признака 
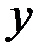от теоретических 
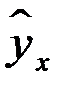минимальна:
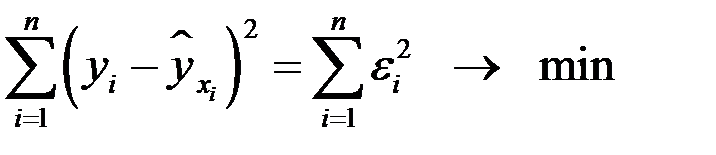Метод наименьших квадратов (МНК) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функцией. Суть метода наименьших квадратов (МНК).
Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b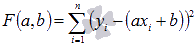 
принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов.
Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.
42. Оценка спецификации модели. Проверка гипотез, относящихся к коэффициентам уравнения парной линейной регрессии.
Под качеством спецификации модели понимается:
- качество выбора функции уравнения регрессии;
- качество выбора набора регрессоров (факторов) 
43. Понятие «временной ряд» и «анализ временного ряда».
Временно́й ряд (или ряд динамики) — собранный в разные моменты времени статистический материал о значении каких-либо параметров (в простейшем случае одного) исследуемого процесса. Каждая единица статистического материала называется измерением или отсчётом, также допустимо называть его уровнем на указанный с ним момент времени. Во временном ряде для каждого отсчёта должно быть указано время измерения или номер измерения по порядку. Временной ряд существенно отличается от простой выборки данных, так как при анализе учитывается взаимосвязь измерений со временем, а не только статистическое разнообразие и статистические характеристики выборки.
Ана́лиз временны́х рядо́в — совокупность математико-статистических методов анализа, предназначенных для выявления структуры временных рядов и для их прогнозирования. Сюда относятся, в частности, методы регрессионного анализа. Выявление структуры временного ряда необходимо для того, чтобы построить математическую модель того явления, которое является источником анализируемого временного ряда. Прогноз будущих значений временного ряда используется для эффективного принятия решений.
Временные ряды состоят из двух элементов:
· периода времени, за который или по состоянию на который приводятся числовые значения;
· числовых значений того или иного показателя, называемых уровнями ряда.
44. Понятие «корреляционный анализ»
