Основные понятия математической статистики

Математическая статистика (МС) – прикладной раздел теории вероятностей (ТВ). Поэтому предмет изучения у них общий. ТВ и МС изучают закономерности в случайных явлениях (процессах). Вместе с тем ТВ изучает непосредственно не сами реальные случайные явления окружающего мира, а их абстрактные математические модели. При этом в задачах ТВ предполагается, что вероятностное пространство заранее задано. Однако в практических задачах в большинстве своем положение совершенно иное: как правило, априори законы распределения неизвестны. Единственное, что мы можем сделать при изучении случайных явлений – это ставить эксперименты (опыты) и производить наблюдения за случайными явлениями. Именно МС работает с экспериментальными данными и помогает восстановить строение вероятностного пространства, на основе чего строится вероятностная модель, адекватная реальному случайному явлению. Итак, в узком смысле МС изучает методы обработки экспериментальных данных с целью получения достоверной информации об интересующем исследователя случайном явлении (процессе). МС обеспечивает ТВ необходимой информацией для построения адекватной реальному процессу вероятностной модели, с помощью которой ТВ не только выявляет объективные закономерности, но и помогает осуществлять научный прогноз в своеобразной области случайных явлений.

Перечислим основные задачи МС:

1) первичная обработка результатов наблюдений (эксперимента);

2) проверка статистических гипотез;

3) статистические оценки параметров распределения;

4) исследование статистических зависимостей (связей).

Генеральная совокупность – множество всех объектов (субъектов), подлежащих изучению.

Выборочная совокупность (выборка) – ограниченное подмножество объектов, отобранных из генеральной совокупности.

Примем следующие обозачения:

N – объем генеральной совокупности (т.е. число объектов этой совокупности);

n – объем выборки.

Понятно, что объем выборки значительно меньше объема генеральной совокупности 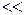(n N).

Суть выборочного метода статистического исследования некоторого признака C генеральной совокупности состоит в том, что по результатам обследования объектов выборки требуется сделать объективное заключение о признаке C всей генеральной совокупности. Но для этого выборка должна правильно представлять генеральную совокупность. Поэтому к выборке должны быть предъявлены определенные требования (они будут проясняться по мере развития необходимого аппарата). Здесь же мы отметим только основной принцип формирования выборки – принцип случайного отбора: выборка должна быть организована таким образом, чтобы каждый объект генеральной совокупности имел одинаковые шансы попасть в эту выборку.

Пусть из генеральной совокупности объема N для изучения некоторого признака (случайной величины) Cизвлечена выборка объема n и в результате проведенного обследования объектов выборки обнаружилось, что значение 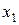признака Cнаблюдалось 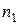, 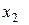– 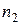,…, 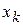– 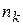раз. Очевидно, 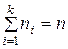. Расположим все наблюдаемые значения 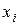признака C 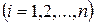в неубывающем порядке:

.

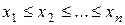Вариационным рядом называется последовательность наблюдаемых значений признака C, расположенных в неубывающем порядке:

.

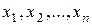Каждое значение 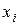вариационного ряда называется вариантой.

Числа 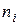наблюдений различных вариант 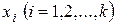называются частотами этих вариант, а отношения 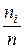(где n – объем выборки) называются относительными частотами соответствующих вариант и обозначаются через 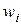. Итак, .

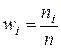Заметим, что 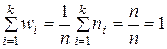, т.е. сумма относительных частот вариант равна 1.

Статистическим рядом называется таблица следующего вида:

			…
			…

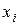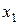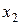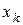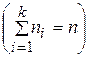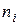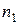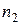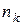В первой строке таблицы записываются различные варианты, а во второй – соответствующие им частоты. Здесь 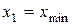(наименьшая варианта), 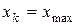(наибольшая варианта). Разность 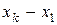обычно обозначают через R и называют размахом выборки: .

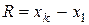Выборочный ряд распределения задается с помощью следующей таблицы:

			…
			…

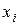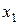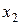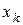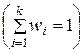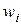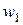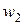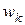В ней указывается соответствие между наблюдаемыми вариантами 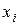и их относительными частотами 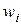. Отметим, что выборочный ряд распределения является аналогом ряда распределения дискретной случайной величины.

Полигоном частот называется графическое изображение статистического ряда (рис.1).

Рисунок 1 – Полигон частот

По оси абсцисс откладываются различные варианты 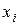, а по оси ординат соответствующие им частоты 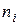. Ломаная линия, соединяющая точки 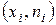, является полигоном частот.

Полигон относительных частот – графическое представление выборочного ряда распределения (рис.2).

Рисунок 2 - Полигон относительных частот

Заметим, что полигон относительных частот является аналогом многоугольника распределения дискретной случайной величины.

Эмпирическая функция распределения

Эмпирической функцией распределения признака Cназывается функция 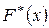, значением которой при каждом фиксированном значении аргумента x является относительная частота события 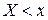, т.е. функция вида

,

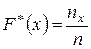где 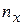– число вариант, меньших рассматриваемого значения аргумента x (причем здесь каждая варианта считается столько раз, сколько она наблюдалась);

n – объем выборки.

Свойства 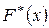аналогичны свойствам теоретической функции распределения 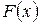и вытекают непосредственно из определения :

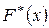1. Значения эмпирической функции распределения заключены между 0 и 1: ;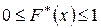

2. 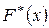есть неубывающая функция;

3. 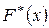=0 при 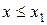( 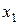– наименьшая варианта),

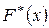=1 при 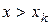( 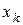– наибольшая варианта).

Общий вид графика эмпирической функции распределения приведен на рис.3.

Рисунок 3 - Общий вид графика эмпирической фукции распределеия

Заметим, что эмпирическая функция распределения 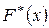служит в качестве подходящего приближенного описания теоретической функции распределения 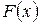изучаемого признака C генеральной совокупности.