Размах выборки, мода и медиана
Размах выборки 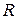 (см. п.2.1.2.2.):
(см. п.2.1.2.2.): 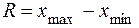 .
.
Определение же моды 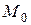 и медианы
и медианы 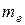 распределения удобно провести в зависимости от типа группировки выборочных данных.
распределения удобно провести в зависимости от типа группировки выборочных данных.
Случай безинтервальной группировки
Модой 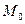 называется варианта с наибольшей частотой.
называется варианта с наибольшей частотой.
Медиана 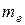 – варианта, которая делит вариационный ряд на две части, равные по числу вариант.
– варианта, которая делит вариационный ряд на две части, равные по числу вариант.
Рассмотрим ряд примеров.
Пример 1. Для вариационного ряда 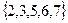 ,
, 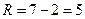 ,
, 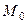 – любая из вариант,
– любая из вариант, 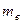 =5.
=5.
Пример 2. Для вариационного ряда 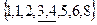 ,
, 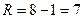 ,
, 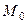 =1, а в качестве
=1, а в качестве 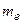 удобно принять среднее арифметическое выделенных вариант:
удобно принять среднее арифметическое выделенных вариант: 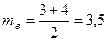 .
.
Пример 3. Для статистического ряда
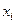 | 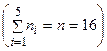 | |||||
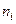 |
R =19–15=4, 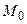 =18,
=18, 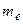 =17.
=17.
Случай интервальной группировки
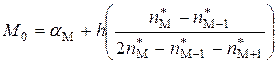 ,
,
где 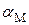 – левая граница интервала, имеющего наибольшую интервальную частоту;
– левая граница интервала, имеющего наибольшую интервальную частоту;
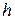 – шаг (длина интервала группировки),
– шаг (длина интервала группировки), 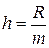 ;
;
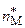 – наибольшая интервальная частота;
– наибольшая интервальная частота;
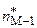 – интервальная частота интервала, расположенного слева от интервала с наибольшей частотой;
– интервальная частота интервала, расположенного слева от интервала с наибольшей частотой;
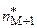 – интервальная часть интервала, лежащего справа от интервала с наибольшей частотой.
– интервальная часть интервала, лежащего справа от интервала с наибольшей частотой.
Формула для нахождения медианы распределения имеет вид
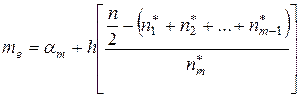 ,
,
где 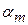 – левая граница интервала, содержащего медиану;
– левая граница интервала, содержащего медиану;
h – шаг;
n – объем выборки;
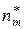 – интервальная частота интервала, содержащего медиану;
– интервальная частота интервала, содержащего медиану;
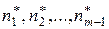 – интервальные частоты интервалов, расположенных слева от интервала, содержащего медиану.
– интервальные частоты интервалов, расположенных слева от интервала, содержащего медиану.
Пример 4. Для интервального статистического ряда
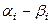 | 14-23 | 23-32 | 32-41 | 41-50 | 50-59 | 59-68 | 68-77 |
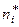 |
n =50, R = 77–14 =63, h =9, m =7.
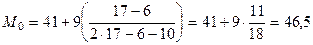 ;
;
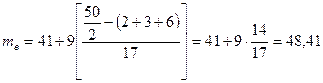 .
.
Выборочная средняя, выборочная дисперсия, выборочное среднее квадратическое отклонение, выборочный коэффициент вариации
Выборочная средняя 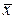 в зависимости от типа группировки выборочных данных определяется по одной из следующих формул:
в зависимости от типа группировки выборочных данных определяется по одной из следующих формул:
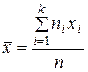 (в случае безинтервальной группировки)
(в случае безинтервальной группировки)
или

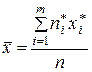 (в случае интервальной группировки).
(в случае интервальной группировки).
Выборочная средняя 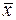 характеризует центр распределения, около которого группируются все варианты.
характеризует центр распределения, около которого группируются все варианты.
Выборочная дисперсия 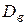 определяется по формуле
определяется по формуле
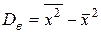 ,
,
которая конкретизируется в зависимости от типа группировки:
· в случае безинтервальной группировки
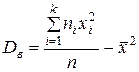 ;
;
· в случае интервальной группировки
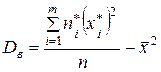 .
.
Выборочная дисперсия 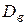 служит характеристикой рассеяния вариационного ряда.
служит характеристикой рассеяния вариационного ряда.
Выборочное среднее квадратическое отклонение 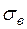 определяется по формуле
определяется по формуле
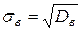
и часто является более удобной характеристикой рассеяния вариационного ряда, так как имеет размерность самой случайной переменной (признака) C.
Еще одна числовая характеристика рассеяния вариационного ряда – выборочный коэффициент вариации 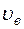 , который определяется по формуле
, который определяется по формуле
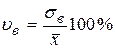 .
.
Эта характеристика является безразмерной величиной (она выражается в процентах) и поэтому ее удобно использовать для сравнения степени рассеяния двух разнородных вариационных рядов.
Метод условных вариант для практического расчета
С целью существенного упрощения "ручных" вычислений выборочной средней 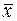 и выборочной дисперсии
и выборочной дисперсии 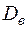 применим так называемый метод условных вариант.
применим так называемый метод условных вариант.
Случай безинтервальной группировки
От исходных вариант 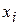 перейдем к "условным вариантам"
перейдем к "условным вариантам" 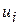 , которые связаны между собой соотношением
, которые связаны между собой соотношением
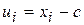 ,
,
где с – "ложный нуль", в качестве которого удобно принять медиану (или варианту, ближайшую к медиане): 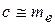 .
.
Интересующие нас характеристики вычисляются по формулам:
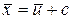 ,
, 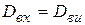 ,
,
где 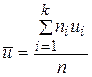 ,
, 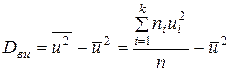 .
.
Случай интервальной группировки
Здесь переход к условным вариантам осуществляется по формуле
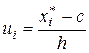 ,
,
где в качестве "ложного нуля" 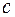 принимается центр того интервала, который содержит медиану:
принимается центр того интервала, который содержит медиану: 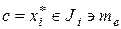 .
.
Интересующие же нас числовые характеристики находятся по формулам: 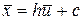 ,
, 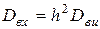 ,
,
где 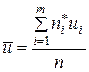 ,
, 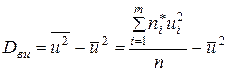 .
.
Пример 1. Дан статистический ряд
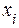 | 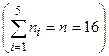 | |||||
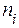 |
Требуется найти 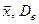 .
.
Применим метод условных вариант для случая безинтервальной группировки при 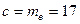 . Вычисления организуем в форме следующей расчетной таблицы:
. Вычисления организуем в форме следующей расчетной таблицы:
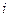 | 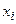 | 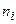 | 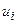 | 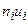 | 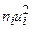 |
| –2 | –2 | ||||
| –1 | –4 | ||||
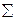 | – | – | |||
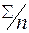 | – | – | 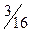 | 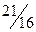 |
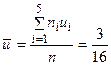 ,
, 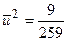 ,
, 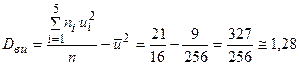 .
.
Тогда 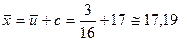 ;
;
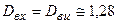 .
.
Пример 2. Дан интервальный статистический ряд
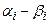 | 14 – 23 | 23 – 32 | 32 – 41 | 41 – 50 | 50 – 59 | 59 – 68 | 68 – 77 | 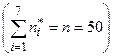 |
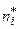 |
Требуется найти 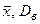 .
.
Применим метод условных вариант для случая интервальной группировки при
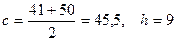 .
.
Вычисления организуем в форме следующей расчетной таблицы:
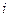 | 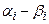 | 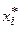 | 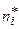 | 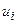 | 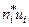 | 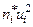 |
| 14–23 | 18,5 | –3 | –6 | |||
| 23–32 | 27,5 | –2 | –6 | |||
| 32–41 | 36,5 | –1 | –6 | |||
| 41–50 | 45,5 | |||||
| 50–59 | 54,5 | |||||
| 59–68 | 63,5 | |||||
| 68–77 | 72,5 | |||||
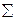 | – | – | – | |||
| å¤ n | – | – | – | 0,38 | 2,18 |
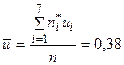 ,
, 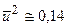 ,
, 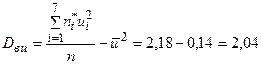 .
.
Тогда 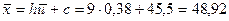 ;
; 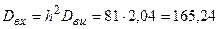 .
.
Квантили распределения и их нахождение
Квантили теоретического распределения
Квантилью порядка р, или р-квантилью, (0< p <1) непрерывной случайной величины Cназывается такое ее возможное значение 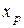 , для которого выполняется равенство
, для которого выполняется равенство
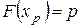 .
.
Здесь 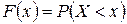 – функция распределения случайной величины C.
– функция распределения случайной величины C.
Графическая интерпретация данного определения представлена на рис. 7.
 |
Рисунок 7 - Графическое определение p -квантили
Частными случаями квантилей являются:
· квартили – квантили 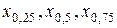 (соответственно 1-я, 2-я и 3-я квартили);
(соответственно 1-я, 2-я и 3-я квартили);
· децили – квантили 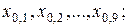
· процентили – квантили 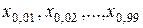 .
.
Квартили 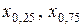 порядков
порядков 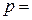 0,25 и
0,25 и 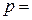 0,75 называются также соответственно нижней и верхней квартилями, разность
0,75 называются также соответственно нижней и верхней квартилями, разность 
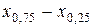 – межквартильным размахом, квартиль
– межквартильным размахом, квартиль 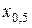 совпадает с медианой
совпадает с медианой 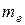 . Аналогичная терминология употребляется и по отношению к децилям и процентилям.
. Аналогичная терминология употребляется и по отношению к децилям и процентилям.
Для стандартных в математической статистике законов распределения, в частности для стандартного нормального распределения 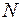 (0;1), имеются специальные таблицы квантилей.
(0;1), имеются специальные таблицы квантилей.
Выборочные квантили и их практическое нахождение
 |
Выборочной квантилью порядка р (0<
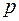 <1) называется абсцисса
<1) называется абсцисса 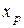 точки пересечения кумулятивной кривой с прямой
точки пересечения кумулятивной кривой с прямой 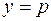 (рис.8).
(рис.8). Рисунок 8 - Графическое определение выборочной квантили порядка p
Это определение дает и способ практического нахождения выборочных квантилей. Однако графическое отыскание квантилей сопровождается погрешностями построений графиков. Во избежание этого целесообразно использовать следующий способ уточненного расчета квантилей, основанный на методе линейной интерполяции.
Рассмотрим соответствующее заданному порядку 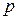 искомой квантили звено кумулятивной кривой (рис.9).
искомой квантили звено кумулятивной кривой (рис.9).
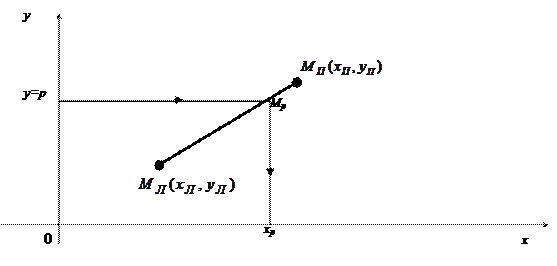 |
Рисунок 9 - Звено кумулятивной кривой
Заменяя, согласно линейной интерполяции, кумулятивную кривую на участке 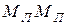 отрезком прямой, находим
отрезком прямой, находим
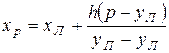 .
.
Пример. Дан интервальный статистический ряд
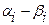 | 50 – 53 | 53 – 56 | 56 – 59 | 59 – 62 | 62 – 65 | 65 – 68 | 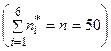 |
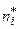 |
Требуется найти нижнюю и верхнюю квартили, а также 4-ю и 6-ю децили.
Предварительно составим таблицу:
 | 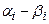 | 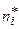 | 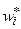 | 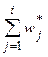 |
| 50–53 | 0,02 | 0,02 | ||
| 53–56 | 0,04 | 0,06 | ||
| 56–59 | 0,22 | 0,28 | ||
| 59–62 | 0,42 | 0,70 | ||
| 62–65 | 0,22 | 0,92 | ||
| 65–68 | 0,08 | 1,00 | ||
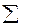 | – | 1,00 | – |
Здесь 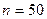 ,
, 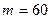 ,
, 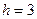 .
.
Опираясь на таблицу, геометрический смысл и расчетную формулу, последовательно находим:
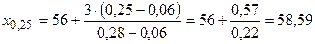 ;
;
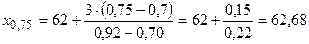 ;
;
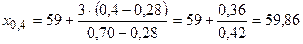 ;
;
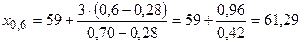 .
.
 2015-01-21
2015-01-21 2627
2627
