Точечные статистические оценки параметров распределения

Понятие точечной оценки

Статистическая оценка параметра теоретического распределения – это его подходящее приближенное значение, полученное по результатам обработки выборки. Статистическая оценка называется точечной, если она выражается одним числом. Так, для параметров 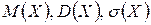теоретического распределения признака C генеральной совокупности их точечными статистическими оценками соответственно являются 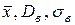– знакомые нам числовые характеристики распределения выборки.

Для того чтобы точечная статистическая оценка имела практическую ценность, т.е. давала хорошее приближение неизвестного параметра распределения признака C генеральной совокупности, она должна удовлетворять ряду требований.

Требования, предъявляемые к точечным статистическим оценкам

Для удобства изложения введем следующие обобщенные обозначения:

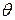– неизвестный параметр теоретического распределения;

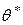– его точная статистическая оценка.

Отметим, что поскольку выборка формируется из генеральной совокупности случайным образом, то оценка 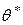, вычисляемая по данным выборки, будет изменяться в зависимости от извлекаемой выборки. Поэтому мы будем рассматривать статистическую оценку 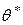как случайную величину; напротив, неизвестный параметр 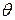есть постоянное число.

Точечная статистическая оценка 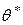называется несмещенной, если ее математическое ожидание равно оцениваемому параметру 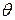, т.е.

.

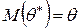Выполнение этого требования страхует от появления систематических ошибок.

Несмещенная статистическая оценка 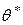называется эффективной, если она имеет наименьшую дисперсию по сравнению с другими возможными оценками того же параметра, полученными по выборке того же объема

.

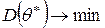Выполнение этого требования означает, что случайные ошибки сведены к минимуму.

Точечная статистическая оценка 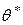называется состоятельной, если она стремится (по вероятности) к оцениваемому параметру 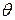при неограниченном увеличении объема выборки, т.е. если для любого сколь угодно малого положительного числа 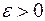выполняется предельное равенство

.

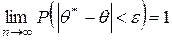Заметим, что если дисперсия несмещенной оценки при 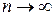стремится к нулю (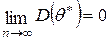), то такая оценка является также состоятельной.

Оказывается, что выборочная средняя 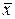является несмещенной, эффективной и состоятельной оценкой для математического ожидания 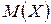признака C генеральной совокупности. Напротив, выборочная дисперсия 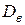не является несмещенной оценкой для неизвестной дисперсии 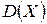признака Cгенеральной совокупности.

2.1.5.3. "Исправленная" дисперсия и "исправленное" среднее квадратическое отклонение

Указанный недостаток точечной оценки 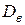можно устранить, введя так называемую " исправленную" дисперсию 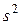, которая выражается формулой:

.

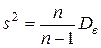Множитель 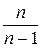называют поправочным коэффициентом. Исправленная дисперсия 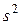является несмещенной, эффективной и состоятельной оценкой для .

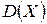Очевидно, при достаточно больших значениях 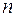выборочная и "исправленная" дисперсии различаются мало. Обычно на практике следует пользоваться "исправленной" дисперсией 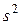при выборках малого объема (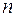 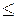30).

Точечную статистическую оценку для среднего квадратичного отклонения 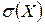, выражаемую формулой 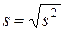, называют "исправленным" средним квадратическим отклонением.