2015-01-21
4691
Если объем выборки достаточно большой (n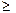 
50), то описанная выше группировка выборочных данных и соответствующие графические представления становятся трудно обозримыми. Поэтому нужно проводить интервальную группировку.
Интервальный статистический ряд и полигон интервальных частот. Интервальный выборочный ряд распределения и полигон интервальных относительных частот
Разобьем весь диапазон наблюдаемых значений вариант (отрезок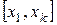 
) на m интервалов равной длины 
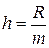(h – шаг):
; 
; 
; 
.
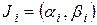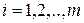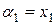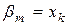Обозначим через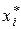 
– середину (центр) i -го интервала:
.
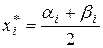
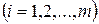Обозначим через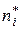 
– количество вариант, попадающих в 
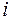-й интервал 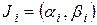, при этом каждая варианта считается столько раз, сколько она наблюдалась. Если варианта совпадает с правым концом рассматриваемого интервала, то ее относят к следующему интервалу.
Величины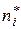 
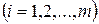назовем интервальными частотами; очевидно, 
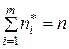. Величины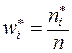 
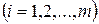– интервальными относительными частотами; 
.
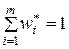Интервальным статистическим рядом является таблица вида:
| |  |  | … |  |  |
| |  |  | … |  |
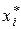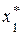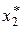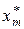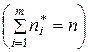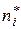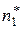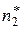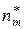Графическое изображение таблицы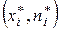 
называется полигоном интервальных частот.
Интервальный выборочный ряд распределения – это таблица следующего вида:
| | | | … | |  |
 |  |  | … |  |
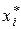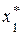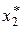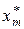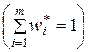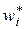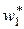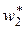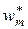Графическое представление таблицы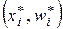 
есть полигон интервальных относительных частот.
Гистограмма частот и гистограмма относительных частот
Предположим, что выполнена интервальная группировка и получены интервальный статистический ряд и интервальный выборочный ряд распределения. На каждом из интервалов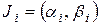 
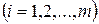одинаковой длины h, как на основании, построим прямоугольник, площадь которого 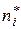, т.е. высота которого равна 
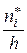. В результате получим ступенчатую фигуру, которая и называется гистограммой частот (рис.4.).
Если же на каждом интервале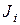 
как на основании построить прямоугольник с площадью 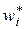(т.е. с высотой 
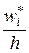), то полученная в результате этого ступенчатая фигура будет называться гистограммой относительных частот (рисунок 5).
 |
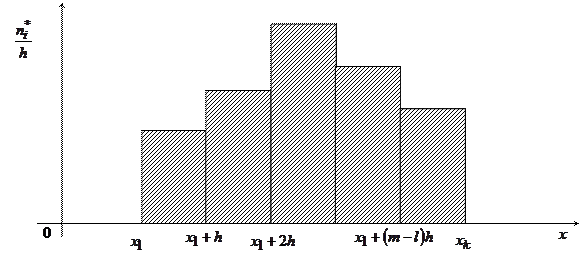Рисунок 4 - Гистограмма частот
 |
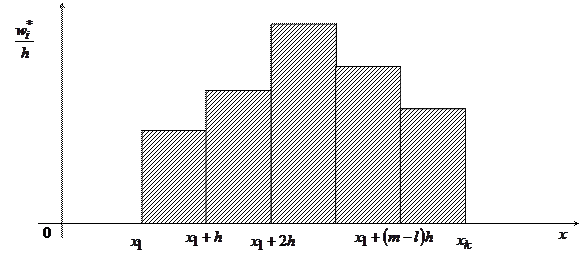Рисунок 5 - Гистограмма относительных частот
Гистограмма относительных частот дает приближенное представление о кривой распределения признака C(т.е. о графике плотности распределения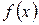 
).
Кумулятивная кривая
Для каждого интервала группировки 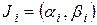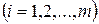вычислим соответствующую накопленную интервальную относительную частоту 
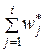, т.е. сумму интервальных относительных частот 
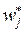в интервалах, лежащих слева от 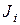, и в данном рассматриваемом интервале .
 |
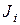Кумулятивной кривой называется ломаная линия с вершинами в точках
; 
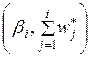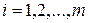, где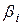 
– правый конец 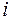-го интервала группировки. (рис.6.) Рисунок 6 - Кумулятивная кривая
Заметим, что кумулятивная кривая является подходящим приближенным представлением для графика функции распределения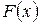 
изучаемого признака C.
В заключение отметим, что число интервалов группировки m обычно выбирается от 6 до 20. Имеются компьютерные статистические программы, которые позволяют автоматизировать процесс составления таблиц и построения графиков.
