Комбинированный инверсный код

В таком коде к исходной 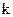-разрядной комбинации добавляется еще 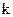контрольных символов. Правило образования кода следующее: если в исходной комбинации четное число единиц, то добавляемая комбинация повторяет исходную, если нечетное, то дополнительная комбинация – инвертированная исходная.

Пример.

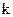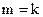		Инверсный код
1 1 0 0 0 1	0 0 1 1 1 0	1 1 0 0 0 1 0 0 1 1 1 0
0 0 1 0 1 0	0 0 1 0 1 0	0 0 1 0 1 0 0 0 1 0 1 0

Прием комбинированного инверсного кода осуществляется в два этапа.

На 1-ом этапе суммируются единицы в первой (основной) группе символов 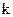. Если число единиц в этой части комбинации четное, то последующие контрольные символы принимаются без изменения; если число символов окажется нечетное, то контрольные символы инвертируются.

На 2-ом этапе контрольные символы 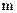сравниваются с информационными 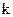(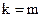) путем суммирования по модулю 2. Если передача прошла без ошибок, то результат суммирования будет нулевым. В противном случае в сумме по модулю 2 появляются единицы, что и является индикатором ошибки.

Корректирующая способность кода очень высокая. Например, если в информационной части исказилось нечетное число разрядов, то ошибка будет не обнаружена только в случае, когда в проверочной части разряды, соответствующие ошибочным информационным, сохраняются неизмененными., а все остальные разряды инвертируются. Если же в информационной части искажается четное число разрядов, то ошибка не обнаруживается, когда будут искажены одноименные разряды и в проверочной части. Вероятность появления таких событий мала.

Рассматриваемый код способен не только обнаруживать многократные ошибки, но и исправлять однократные. При этом индикатором ошибочного разряда в информационной части является 0 при 1 во всех остальных разрядах суммы по 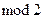, а индикатором ошибочного разряда в проверочной части является 1 при 0 во всех остальных разрядах указанной суммы.

Пример.

Пусть исходная комбинация имеет вид:

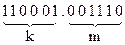
Предположим, что произошла однократная ошибка в информационной части, т.е. принята комбинация

.

После декодирования получаем:

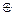							– чт
							Вывод: ошибка в 4-м разряде информа-
							ционной части.

Если принята комбинация 1

.

0,

т.е. произошла ошибка в контрольной части, после декодирования получаем:

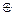							– нч
							Вывод: ошибка в 5-м разряде провероч-
							ной части.

Комбинированный инверсный код относится к группе разделимых и систематических.

2.5. Линейные коды, обнаруживающие
и исправляющие ошибки.

Линейными называют коды, в которых проверочные символы представляют собой линейные комбинации информационных символов, т.е. линейные коды являются систематическими.

Основой математического описания линейных кодов является теория алгебраических систем (теория групп, колец, полей, векторных пространств, матриц).

Кодовые комбинации в линейных кодах рассматриваются как элементы множества.

Алгебраическими системами называют множества, для которых определены некоторые алгебраические операции. Под алгебраической операцией понимается однозначное сопоставление двум элементам третьего элемента по определенным правилам. Обычно такой операцией является сложение (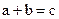) или умножение ().

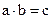Рассмотрим кратко такие алгебраические системы, как группа и кольцо.

Группой называется множество элементов (кодовых комбинаций), объединенных определенным законом композиции. Это значит, что задана некоторая операция 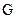, в результате применения которой к любым двум комбинациям группы образуется третья комбинация, также принадлежащая этой группе. Иными словами, группа – это множество кодовых слов, обладающих свойством замкнутости относительно операции .

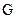Если операция, определенная в группе, коммутативна, т.е. справедливо равенство 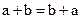(для группы с операцией сложения) или равенство 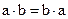(для группы с операцией умножения), то группа называется коммутативной или абелевой.

Группа, состоящая из конечного числа элементов, называется конечной.

Чтобы множество n-разрядных кодовых комбинаций, было конечной группой, при выполнении основной операции число разрядов в результирующей комбинации не должно увеличиваться. Этому условию удовлетворяет операция символического поразрядного сложения по заданному модулю 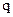, при которой цифры одинаковых разрядов элементов группы (кодовых комбинаций) складываются обычным порядком, а результатом сложения считается остаток от деления полученного числа на модуль .

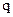Кроме отмеченного, элементы группы должны удовлетворять следующим требованиям:

– для любых трех элементов группы a, b и c должен выполняться закон ассоциативности, т.е. 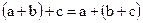(если основная операция – сложение) и 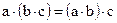(если основная операция – умножение);

– существует нулевой элемент 0 со свойством 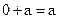(в группе операций сложения) и единичный элемент 1 со свойством 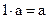(в группе с операцией умножения);

– для каждого элемента 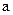группы существует противоположный элемент, обозначаемый – 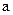, со свойством – 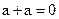(для группы по сложению), и обратный элемент, обозначаемый 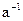, со свойством 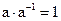(для группы по умножению).

В теории двоичных кодов рассматриваются аддитивные группы, т.е. группы с операцией сложения (по модулю 2).

Кольцом называется множество элементов 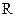, на котором определены две операции – сложения и умножения, такие, что:

– множество 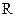является коммутативной группой по сложению;

– произведение элементов 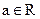и 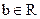есть элемент множества 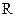(замкнутость по отношении к умножению);

– для любых трех элементов a, b и c из 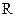справедливо равенство 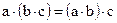(ассоциативный закон для умножения);

– для любых трех элементов a, b и c из 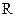выполняются соотношения 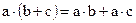и 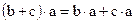(дистрибутивные законы).

Более подробно теория рассмотренных и прочих алгебраических систем излагается в работах [1] и [6].