Когда речь идет о линейных кодах, кодовые комбинации принято называть кодовыми векторами (КВ).
Линейный код обычно обозначают как 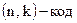 , где
, где 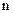 – значность КВ,
– значность КВ, 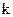 – число информационных символов. Следовательно, число проверочных (контрольных) символов
– число информационных символов. Следовательно, число проверочных (контрольных) символов 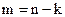 .
.
Построение линейного 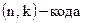 начинается с выбора числа информационных разрядов в кодовых векторах. Это число выбирается, исходя из требуемого объема кода
начинается с выбора числа информационных разрядов в кодовых векторах. Это число выбирается, исходя из требуемого объема кода 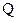 , т.е. максимального числа сообщений, которое требуется передавать.
, т.е. максимального числа сообщений, которое требуется передавать.
В случае передачи двоичным кодом величина 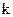 должна удовлетворять неравенству:
должна удовлетворять неравенству:
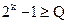 (2.23)
(2.23)
(единица вычитается из 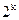 потому, что нулевая комбинация обычно не используется при передаче, т.к. не изменяет состояния канала).
потому, что нулевая комбинация обычно не используется при передаче, т.к. не изменяет состояния канала).
После выбора 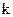 определяется число контрольных разрядов
определяется число контрольных разрядов 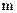 , необходимое для получения требуемой корректирующей способности кода.
, необходимое для получения требуемой корректирующей способности кода.
Если требуется исправлять все одиночные ошибки (кодовое расстояние кода 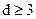 ), величина
), величина 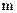 выбирается из следующих соображений. Под действием помех может быть искажен любой символ в n-значном КВ, т.е. для каждого кодового вектора возможно
выбирается из следующих соображений. Под действием помех может быть искажен любой символ в n-значном КВ, т.е. для каждого кодового вектора возможно 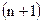 исходов передачи (
исходов передачи (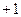 учитывает правильную передачу). С помощью контрольных символов нужно различать все возможные исходы передачи. Это возможно, если выполняется условие:
учитывает правильную передачу). С помощью контрольных символов нужно различать все возможные исходы передачи. Это возможно, если выполняется условие:
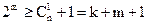 , (2.24)
, (2.24)
где 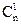 – число сочетаний из
– число сочетаний из 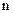 по 1.
по 1.
Уравнение (2.24) является трансцендентным относительно 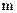 , поэтому при небольших
, поэтому при небольших 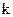 величину
величину 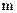 определяют простым подбором, принимая максимальное значение
определяют простым подбором, принимая максимальное значение 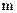 , удовлетворяющие (2.24).
, удовлетворяющие (2.24).
При больших 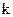 для определения
для определения 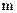 при
при 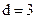 можно использовать эмпирическое соотношение:
можно использовать эмпирическое соотношение:
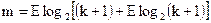 , (2.25)
, (2.25)
где 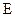 – знак округления до ближайшего большего числа.
– знак округления до ближайшего большего числа.
Если необходимо исправлять не только все единичные, но и все двойные независимые ошибки, величина 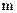 должна выбираться в соответствии с условием:
должна выбираться в соответствии с условием:
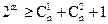 . (2.26)
. (2.26)
В общем случае для исправления всех независимых ошибок кратности до 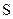 включительно
включительно
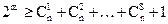 . (2.27)
. (2.27)
После определения 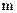 составляется образующая матрица, состоящая из
составляется образующая матрица, состоящая из 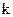 строк и
строк и 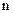 столбцов. В общем виде образующая матрица имеет вид:
столбцов. В общем виде образующая матрица имеет вид:
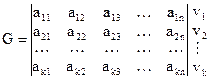 (2.28)
(2.28)
Кодовые векторы, входящие в образующую матрицу, являются исходными разрешенными. Поскольку двоичный линейный код является групповым по сложению, остальные разрешенные КВ получаются путем суммирования по модулю 2 строк образующей матрицы сначала попарно, затем по три, наконец, всех 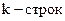 .
.
В качестве строк образующей матрицы могут быть взяты любые КВ, отвечающие следующим условиям. Они должны быть:
1) n-значными;
2) отстоящими друг от друга на заданное кодовое расстояние;
3) ненулевыми;
4) иметь вес не менее заданного кодового расстояния кода;
5) линейно-независимыми.
КВ матрицы 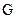 являются разрешенными, что и объясняет первые два требования.
являются разрешенными, что и объясняет первые два требования.
Третье требование связано с тем, что любой групповой код по сложению имеет нулевой элемент, представляющий собой КВ из одних нулей. При сложении такого КВ с любым другим, результат будет совпадать с вторым слагаемым, что недопустимо, т.к. при этом не выполняется требование замкнутости по операции сложения.
Четвертое требование объясняется тем, что КВ образующей матрицы 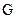 являются разрешенными и, следовательно, должны удовлетворять условию (2.21). Кодовое расстояние между двумя любыми КВ равно весу
являются разрешенными и, следовательно, должны удовлетворять условию (2.21). Кодовое расстояние между двумя любыми КВ равно весу 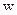 вектора, полученного в результате их сложения по модулю 2. Но нулевой КВ, не входящий в
вектора, полученного в результате их сложения по модулю 2. Но нулевой КВ, не входящий в 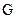 , также является разрешенным. Отсюда следует, что вес КВ, входящих в матрицу
, также является разрешенным. Отсюда следует, что вес КВ, входящих в матрицу  , должен быть не менее заданного кодового расстояния кода.
, должен быть не менее заданного кодового расстояния кода.
Пятое требование гарантирует, что ни один из векторов образующей матрицы (2.28) не будет результатом суммирования по модулю 2 каких-либо других векторов этой же матрицы (в противном случае не будет получено требуемое число разрешенных КВ).
Линейно-независимыми являются КВ, для которых выполняется неравенство:
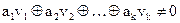 , (2.29)
, (2.29)
где 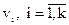 – кодовые векторы;
– кодовые векторы; 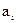 – коэффициенты, принимающие произвольные значения 0 и 1 за исключением
– коэффициенты, принимающие произвольные значения 0 и 1 за исключением 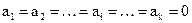 .
.
Последним шагом в построении линейного кода является составление проверочной (контрольной) матрицы, имеющей n столбцов и m строк. В общем виде контрольная матрица имеет вид:
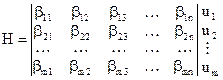 (2.30)
(2.30)
Элементы 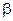 , составляющие контрольную матрицу, представляют собой элементы КВ, ортогональных любым разрешенным кодовым векторам. Если обозначить через V-разрешенные КВ данного линейного кода, а через U-вектор контрольной матрицы, то условие ортогональности КВ V и U в математической форме записывается так:
, составляющие контрольную матрицу, представляют собой элементы КВ, ортогональных любым разрешенным кодовым векторам. Если обозначить через V-разрешенные КВ данного линейного кода, а через U-вектор контрольной матрицы, то условие ортогональности КВ V и U в математической форме записывается так:
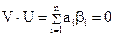 , (2.31)
, (2.31)
где 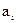 и
и 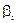 ,
, 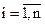 , – соответственно, элементы разрешенных КВ и векторов контрольной матрицы.
, – соответственно, элементы разрешенных КВ и векторов контрольной матрицы.
Кроме того, что любой вектор контрольной матрицы должен быть ортогонален любому разрешенному КВ, матрица 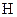 в целом должна удовлетворять следующему требованию: в контрольной матрице не должно быть нулевых и одинаковых столбцов.
в целом должна удовлетворять следующему требованию: в контрольной матрице не должно быть нулевых и одинаковых столбцов.
После построения контрольной матрицы линейный код является полностью определенным. На этапе кодирования КВ формируется так, чтобы он был ортогонален каждому из векторов контрольной матрицы, а на этапе декодирования принятый КВ, возможно содержащий ошибки, проверяется на ортогональность векторам матрицы H.
Пример.
Построить линейный 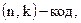 позволяющий исправлять все одиночные ошибки, если требуемый объем кода
позволяющий исправлять все одиночные ошибки, если требуемый объем кода 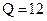 .
.
Решение.
1. Определяем требуемое число информационных разрядов. Согласно (2.23) имеем: 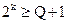 ,
, 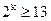 , откуда
, откуда 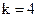 .
.
2. В соответствии с (2.25) определяем требуемое число контрольных разрядов:
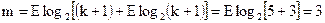 ,
, 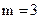 .
.
Следовательно, 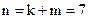 , а код имеет формат (7, 4).
, а код имеет формат (7, 4).
3. Составляем образующую матрицу  .
.
Так как линейный код должен исправлять однократные ошибки, то кодовое расстояние между комбинациями образующей матрицы должно удовлетворять условию (2.21):
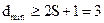 ,
, 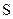 – кратность исправляемой ошибки,
– кратность исправляемой ошибки, 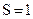 .
.
Теперь, учитывая изложенные выше общие требования к КВ образующей матрицы, переходим к построению самой матрицы. Существует несколько подходов к построению G. В самом общем случае при построении G предварительно не определяют места расположения информационных и контрольных символов. Это становится ясным только после построения контрольной матрицы. Такой подход осуществляется в [10]. В некоторых работах предлагается сразу же назначать места расположения контрольных символов. Так, например, в [7] для кода (7.4) предлагается такое построение кодовых векторов:
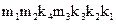 .
.
По мнению автора такая структура КВ несколько упрощает алгоритм определения контрольных символов.
В дальнейшем при построении G будем следовать методике, изложенной в [10].
Пусть образующая матрица имеет вид:
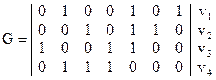
Входящие в нее векторы удовлетворяют всем сформулированным выше условиям.
4. Строим контрольную матрицу H.
Ранее отмечалось, что все КВ контрольной матрицы должны быть ортогональны всем разрешенным комбинациям данного линейного кода.
Кодовые векторы образующей матрицы – разрешенные.
Контрольная матрица 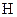 содержит три КВ и, следовательно, для ее построения в соответствии с (2.31) достаточно иметь три разрешенных КВ. Возьмем в качестве таковых векторы
содержит три КВ и, следовательно, для ее построения в соответствии с (2.31) достаточно иметь три разрешенных КВ. Возьмем в качестве таковых векторы 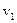 ,
, 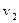 и
и 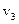 образующей матрицы G.
образующей матрицы G.
Определим условия, при которых любой КВ матрицы 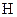 будет ортогонален любому из указанных разрешенных КВ.
будет ортогонален любому из указанных разрешенных КВ.
В соответствии с (2.31) имеем:
| 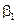
| 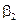
| 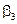
| 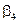
| 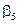
| 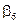
| 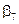
| – 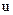
| ||||||
– 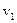
| ||||||||||||||

| 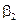
| 
| 
| 
| 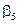
| 
| 
| 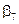
| = 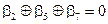
|
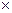
| 
| 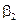
| 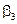
| 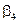
| 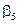
| 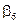
| 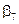
| – 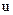
| ||||||
– 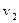
| ||||||||||||||

| 
| 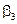
| 
| 
| 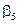
| 
| 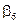
| 
| = 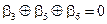
|
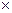
| 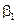
| 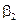
| 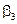
| 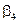
| 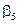
| 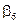
| 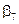
| – 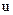
| ||||||
– 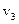
| ||||||||||||||
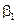
| 
| 
| 
| 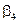
| 
| 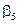
| 
| 
| = 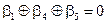
|
Итак, для того, чтобы любой КВ матрицы 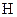 был ортогонален любому разрешенному КВ, векторы контрольной матрицы должны удовлетворять следующим условиям:
был ортогонален любому разрешенному КВ, векторы контрольной матрицы должны удовлетворять следующим условиям:
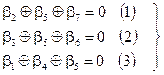 (2.32)
(2.32)
Теперь необходимо подобрать 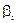 ,
, 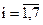 , принимающие значения 0 и 1, так, чтобы они удовлетворяли соотношениям (2.32). При этом необходимо следить, чтобы в контрольной матрице не оказалось нулевых и одинаковых столбцов.
, принимающие значения 0 и 1, так, чтобы они удовлетворяли соотношениям (2.32). При этом необходимо следить, чтобы в контрольной матрице не оказалось нулевых и одинаковых столбцов.
Пусть 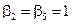 , тогда из (1) следует, что
, тогда из (1) следует, что 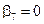 .
.
Если 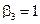 , тогда, согласно (2),
, тогда, согласно (2), 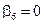 .
.
При 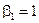 ,
, 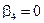 , что следует из (3).
, что следует из (3).
Итак, первый КВ контрольной матрицы определен: 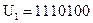 .
.
Определение 2-го КВ контрольной матрицы осуществляется аналогично.
Пусть 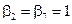 , тогда
, тогда 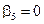
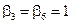
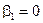 , тогда
, тогда 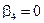 .
.
Принять 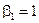 было нельзя, так как тогда первые два символа в столбцах 1, 2 и 3 разрядов были бы единичными, а это привело бы в дальнейшем к появлению одинаковых столбцов в контрольной матрице, что недопустимо. Итак,
было нельзя, так как тогда первые два символа в столбцах 1, 2 и 3 разрядов были бы единичными, а это привело бы в дальнейшем к появлению одинаковых столбцов в контрольной матрице, что недопустимо. Итак, 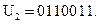
При выборе 3-го КВ контрольной матрицы нужно ввести ряд ограничений, предотвращающих появление одинаковых и нулевых столбцов. В рассматриваемом случае указанные ограничения имеют вид:
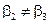 ,
, 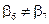 ,
, 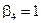 .
.
Тогда, если 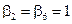 , то
, то 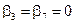 .
. 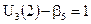 , а из
, а из 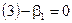 . Итак,
. Итак, 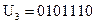 .
.
Контрольная матрица в окончательном виде:
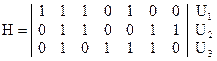 (2.33)
(2.33)
 2015-01-21
2015-01-21 514
514








