Приведем решения:
а) уравнений первой степени
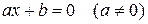 , (1)
, (1)
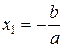 ;
;
б) квадратных уравнений
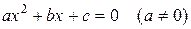 , (2)
, (2)
1) 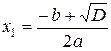 и
и 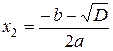 при
при 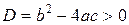 ;
;
2) 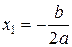 – корень кратности 2 при
– корень кратности 2 при 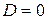 ;
;
3) нет корней при 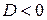 .
.
При решении уравнений степени больше двух используют следующие приемы:
1. Вынесение общего множителя за скобки.
2. Метод группировки. Члены многочлена объединяются в группы так, чтобы в каждой группе можно было получить множитель, общий для всех групп.
3. Использование формул сокращенного умножения.
4. Комбинирование выше перечисленных приемов.
5. С помощью нахождения корней многочлена.
Пусть 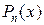 – многочлен n -й степени и
– многочлен n -й степени и 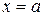 – корень этого многочлена. Тогда, по следствию из теоремы Везу, многочлен
– корень этого многочлена. Тогда, по следствию из теоремы Везу, многочлен 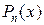 делится без остатка на двучлен
делится без остатка на двучлен 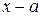 . Следовательно, можно записать равенство
. Следовательно, можно записать равенство 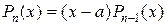 , где
, где 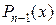 – есть многочлен, равный частному от деления
– есть многочлен, равный частному от деления 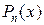 на двучлен
на двучлен 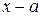 , степень которого на единицу меньше степени многочлена
, степень которого на единицу меньше степени многочлена 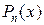 .
.
Пример 1. Решить уравнение 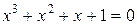 .
.
Решение. 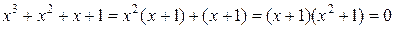 .
.
Ответ: 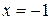 .
.
Пример 2. Решить уравнение 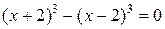 .
.
Решение.
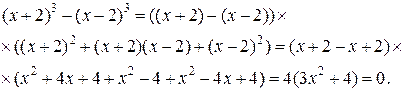
Ответ:нет решений.
Пример 3. Решить уравнение 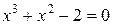 .
.
Решение.Первый способ.
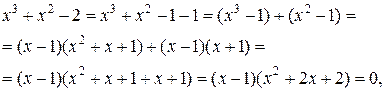
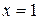 , уравнение
, уравнение 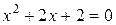 действительных корней не имеет
действительных корней не имеет 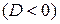 .
.
Второй способ. Методом «подбора» находим корень уравнения 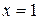 . Следовательно, одним из множителей, на которые разлагается многочлен, будет двучлен
. Следовательно, одним из множителей, на которые разлагается многочлен, будет двучлен 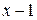 . Разделим многочлен
. Разделим многочлен 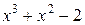 на двучлен
на двучлен 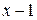 :
:
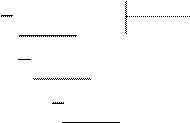 x 3+ x 2–2 x –1
x 3+ x 2–2 x –1
x 3– x 2 x 2+2 x +2
2 x 2–2
2 x 2–2 x
2 x –2
2 x –2
Следовательно, имеем 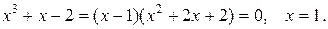
Ответ: 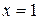 .
.
Решения многих рациональных уравнений заключаются в сведении их тем или иным способом к уравнениям (1) или (2).
Пример 4. Решить уравнение 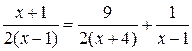 .
.
Решение. О.Д.З. уравнения есть любое x, кроме 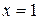 и
и 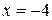 .
.
Исходное уравнение после приведения к общему знаменателю эквивалентно уравнению 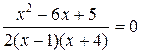 или
или 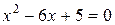 , при условии
, при условии 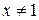 и
и 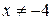 .
.
Решая полученное уравнение, находим, что 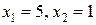 , но
, но 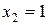 – посторонний корень, так как
– посторонний корень, так как 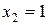 не входит в О.Д.З. неизвестного.
не входит в О.Д.З. неизвестного.
Ответ: 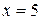 .
.
Одним из приемов сведения рациональных уравнений и уравнений вида (1) и (2) является введение вспомогательного неизвестного.
Пример 5. Решить уравнение 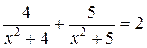 .
.
Решение. Обозначая  , запишем исходное уравнение в виде
, запишем исходное уравнение в виде 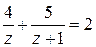 или
или 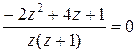 .
.
О.Д.З. уравнения есть любое 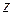 , кроме
, кроме 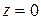 и
и 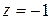 .
.
Последнее уравнение эквивалентно уравнению 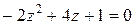 . Эквивалентность этих уравнений следует из того, что корни последнего уравнения
. Эквивалентность этих уравнений следует из того, что корни последнего уравнения 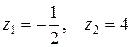 принадлежат О.Д.З. неизвестного. Таким образом, исходное уравнение эквивалентно двум квадратным уравнениям
принадлежат О.Д.З. неизвестного. Таким образом, исходное уравнение эквивалентно двум квадратным уравнениям 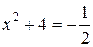 и
и 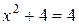 . Корень второго уравнения
. Корень второго уравнения 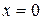 . Первое уравнение действительных корней не имеет.
. Первое уравнение действительных корней не имеет.
Ответ: 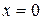 .
.
 2015-01-21
2015-01-21 777
777








