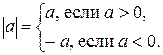
При решении уравнения, содержащего знак абсолютной величины (знак модуля), как правило, следует разбить О.Д.З. уравнения на множества, на каждом из которых выражения, стоящие под знаком модуля, сохраняют знак. На каждом таком множестве уравнение записать без знака модуля и решить на этом множество. Объединение множеств решений, найденных на всех частях О.Д.З. уравнения, составляет множество всех решений уравнения.
Простейшими уравнениями с модулями являются уравнения вида
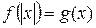 , (1)
, (1)
где 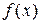 и
и 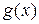 – некоторые функции.
– некоторые функции.
Для того, чтобы решить уравнение (1), нужно найти сначала все решения уравнения 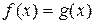 , принадлежащие множеству
, принадлежащие множеству 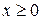 , затем решить уравнение
, затем решить уравнение 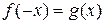 на множестве
на множестве 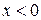 ; объединение множеств найденных решений составляет множество всех решений уравнения (1), т. е. уравнение (1) равносильно совокупности систем
; объединение множеств найденных решений составляет множество всех решений уравнения (1), т. е. уравнение (1) равносильно совокупности систем
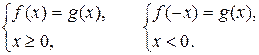
Пример 1. Решить уравнение 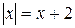 .
.
Решение. Исходное уравнение равносильно совокупности систем
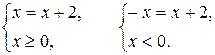
Уравнение  не имеет решений
не имеет решений 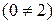 .
.
Уравнение 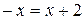 имеет решение
имеет решение 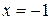 , которое является решением второй системы, так как
, которое является решением второй системы, так как 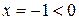 .
.
Ответ: 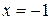 .
.
Уравнение вида
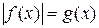 (2)
(2)
равносильно двум совокупностям систем
а) 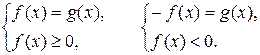
б) 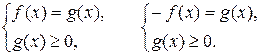
Если в уравнении (2) функция 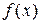 имеет более простой вид, чем
имеет более простой вид, чем 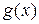 , то целесообразно уравнение (2) заменять первой совокупностью систем, а если более простой вид имеет функция
, то целесообразно уравнение (2) заменять первой совокупностью систем, а если более простой вид имеет функция 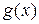 , то уравнение (2) целесообразно заменять второй совокупностью систем.
, то уравнение (2) целесообразно заменять второй совокупностью систем.
Пример 2. Решить уравнение 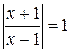 .
.
Решение. Данное уравнение равносильно совокупности уравнений
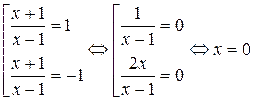 .
.
Ответ: 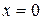 .
.
Пример 3. Решить уравнение 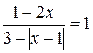 .
.
Решение. Данное уравнение равносильно совокупности двух систем:
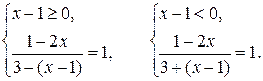
Решая уравнение 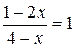 , находим
, находим 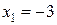 , но это не удовлетворяет условию
, но это не удовлетворяет условию  , поэтому первая система решений не имеет.
, поэтому первая система решений не имеет.
Решая уравнение 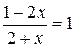 , находим
, находим 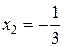 . Это удовлетворяет условию
. Это удовлетворяет условию 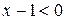 .
.
Ответ: 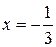 .
.
При решении уравнения, в котором под знаком модуля находится выражение, также содержащее модуль, следует сначала освободиться от внутренних модулей, а затем в полученных уравнениях раскрыть оставшиеся модули.
Пример 4. Решить уравнение  .
.
Решение. Данное уравнение равносильно совокупности двух систем:
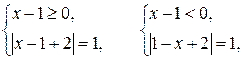
т. е. совокупности систем
 (3)
(3)
Первая система совокупности (3) равносильна совокупности двух следующих систем:
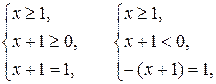
т. е. совокупности
 (4)
(4)
Совокупность (4) решений не имеет.
Вторая система совокупности (3) равносильна совокупности двух следующих систем:
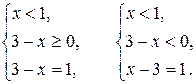 (5)
(5)
Совокупность (5) решений не имеет.
Ответ: нет решений.
Рассмотрим уравнение вида
 , (6)
, (6)
где 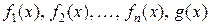 – некоторые функции.
– некоторые функции.
Такие уравнения обычно решают методом интервалов. Для этого находят сначала все точки, в которых хотя бы одна из функций  меняет знак. Эти точки делят область допустимых значений уравнения (6) на промежутки, на каждом из которых все функции
меняет знак. Эти точки делят область допустимых значений уравнения (6) на промежутки, на каждом из которых все функции 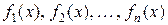 сохраняют знак. Затем, используя определение абсолютной величины, переходят от уравнения (6) к совокупности уравнений, не содержащих знаков модуля.
сохраняют знак. Затем, используя определение абсолютной величины, переходят от уравнения (6) к совокупности уравнений, не содержащих знаков модуля.
Пример 5. Решить уравнение  .
.
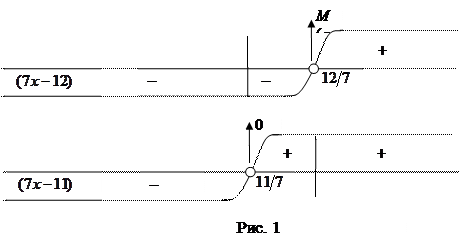
Решение. Методом интервалов (рис. 1) находим интервалы знако-постоянства выражений
 и
и 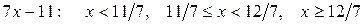 .
.
Итак, данное уравнение эквивалентно следующим уравнениям:
1) 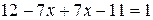 для
для 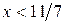 ;
;
2)  для
для 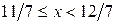 ;
;
3)  для
для 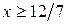 .
.
Первое уравнение обращается в тождество для всех значений 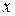 , удовлетворяющих неравенству
, удовлетворяющих неравенству 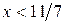 ; второе уравнение имеет решение
; второе уравнение имеет решение 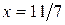 ; третье не имеет решений.
; третье не имеет решений.
Ответ:  .
.
 2015-01-21
2015-01-21 527
527








