VIII. Начала математического анализа. Производная и первообразная функции, ее геометрический и физический смысл.
Пусть на некотором промежутке 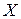 определена некоторая функция
определена некоторая функция 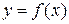
Вычисление производной функции 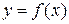 производится по общему правилу дифференцирования:
производится по общему правилу дифференцирования:
1. Придавая аргументу 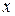 приращение
приращение 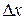 и подставляя в выражение функции вместо аргумента
и подставляя в выражение функции вместо аргумента 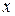 наращенное значение
наращенное значение 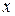 +
+ 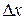 , находим наращенное значение функции:
, находим наращенное значение функции:
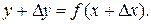
2. Вычитая из наращенного значения функции ее первоначальное значение, находим приращение функции:
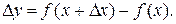
3. Делим приращение функции 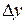 на приращение аргумента
на приращение аргумента 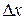 , т.е. составляем отношение:
, т.е. составляем отношение:
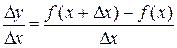 .
.
4. Находим предел этого отношения при 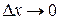 :
:
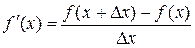 .
.
Этот предел и есть производная от функции 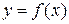 . Итак:
. Итак:
Производной функции f(x) в точке х=х0 называется отношение приращения функции 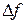 в этой точке к приращению
в этой точке к приращению 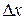 аргумента, при стремлении последнего к нулю.
аргумента, при стремлении последнего к нулю.
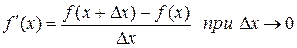 .
.
Нахождение производной называется дифференцированием.
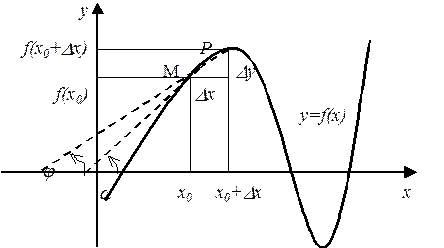
Пусть f(x) определена на некотором промежутке (a, b). Тогда 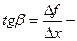 тангенс угла наклона секущей МР к графику функции (рис.10).
тангенс угла наклона секущей МР к графику функции (рис.10).
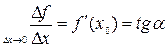 ,
,
где a - угол наклона касательной к графику функции f(x) в точке (x0, f(x0)).
Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.
Уравнение касательной к кривой: 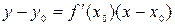
Уравнение нормали к кривой: 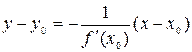 .
.
Фактически производная функции показывает скорость изменения функции, т.е. как изменяется функция при изменении переменной.
Физический смысл производной функции f(t), где t - время, а f(t) - закон движения (изменения координат) – мгновенная скорость движения.
Соответственно, вторая производная функции - скорость изменения скорости, т.е. ускорение.
Основные правила дифференцирования.
Обозначим f(x) = u, g(x) = v - функции, дифференцируемые в точке х.
1) Производная суммы (разности): (u ± v)¢ = u¢ ± v¢
2) Производная произведения: (u×v)¢ = u×v¢ + u¢×v
3) Производная частного: 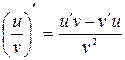 , если v ¹ 0
, если v ¹ 0
4) Производная сложной функции: 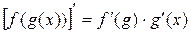
Первообразная функция.
Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство:
F¢(x) = f(x).
Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
F1(x) = F2(x) + C.
Неопределенный интеграл.
Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением:
F(x) + C.
Записывают: 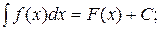
Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.
Свойства:
1. 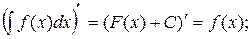
2. 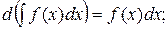
3. 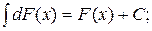
4. 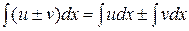 , где u, v, w – некоторые функции от х.
, где u, v, w – некоторые функции от х.
5. 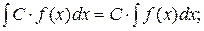
Таблица производных и первообразных некоторых основных элементарных функций.
| № | Первообразная 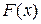
| Функция 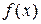
| Производная 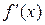
|
| 1. | 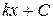
| 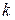
| 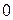
|
| 2. | 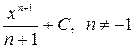
| 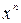
| 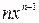
|
| 3. | 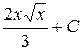
| 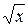
| 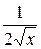
|
| 4. | 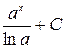
| 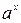
| 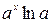
|
| 5. | 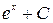
| 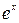
| 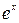
|
| 6. | 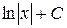
| 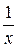
| 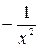
|
| 7. | 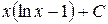
| 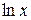
| 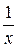
|
| 8. | 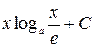
| 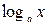
| 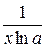
|
| 9. | 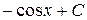
| 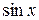
| 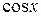
|
| 10. | 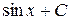
| 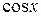
| 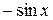
|
| 11. | 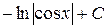
| 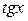
| 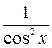
|
| 12. | 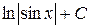
| 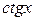
| 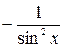
|
| 13. | 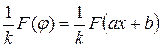
| 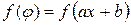
| 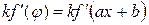
|
Определенный интеграл.
Определенным интегралом функции f(x) от a до b называют разность значений первообразной этой функции в точках a и b.
Формула Ньютона-Лейбница:
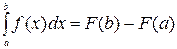 .
.
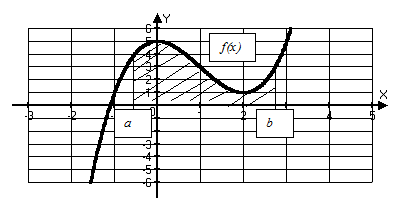
Площадь криволинейной трапеции, ограниченной осью 0X, прямыми 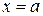 и
и 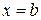 и графиком неотрицательной функции
и графиком неотрицательной функции 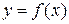 на отрезке
на отрезке 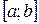 находится по формуле:
находится по формуле:
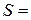
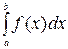 .
.
 Пояснения к разделу: Начала математического анализа
Пояснения к разделу: Начала математического анализа
Приложение производной к исследованию функции.
Возрастание и убывание функции 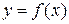 характеризуется знаком ее производной: если в некотором промежутке
характеризуется знаком ее производной: если в некотором промежутке 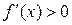 , то функция возрастает в этом промежутке; если же
, то функция возрастает в этом промежутке; если же 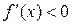 , о функция убывает в этом промежутке.
, о функция убывает в этом промежутке.
Точка 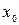 из области определения функции
из области определения функции 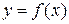 называется точкой минимума этой функции, если существует такая окрестность точки
называется точкой минимума этой функции, если существует такая окрестность точки 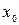 , что для всех точек
, что для всех точек 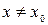 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 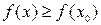 .
.
Точка 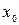 из области определения функции
из области определения функции 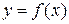 называется точкой максимума этой функции, если существует такая окрестность точки
называется точкой максимума этой функции, если существует такая окрестность точки 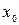 , что для всех точек
, что для всех точек 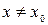 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 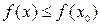 .
.
Точки минимума и максимума функции называются экстремальными точками данной функции, а значения функции в этих точках – минимумом и максимумом функции.
Точками экстремума могут служить только критические точки I рода, т.е. точки принадлежащие области определения функции, в которых производная 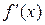 обращается в нуль или терпит разрыв.
обращается в нуль или терпит разрыв.
Если при переходе через критическую точку 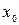 производная
производная 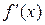 меняет знак, то функция
меняет знак, то функция 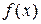 имеет в этой точке экстремум: минимум в том случае, когда производная меняет знак с минуса на плюс, и максимум – когда с плюса на минус. Если же при переходе через критическую точку
имеет в этой точке экстремум: минимум в том случае, когда производная меняет знак с минуса на плюс, и максимум – когда с плюса на минус. Если же при переходе через критическую точку 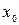 производная не меняет знака, то функция
производная не меняет знака, то функция 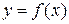 в точке
в точке 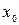 не имеет экстремума.
не имеет экстремума.
Правило нахождения экстремумов функции с помощью производной.
1. Найти производную функции 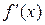 .
.
2. Найти критические точки I рода функции 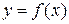 , т.е. точки принадлежащие области определения функции, в которых производная
, т.е. точки принадлежащие области определения функции, в которых производная 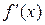 обращается в нуль или терпит разрыв.
обращается в нуль или терпит разрыв.
3. Исследовать знак производной 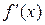 в промежутках, на которые найденные критические точки делят область определения функции
в промежутках, на которые найденные критические точки делят область определения функции 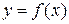 .
.
Рассмотрим два основных метода интегрирования.
Непосредственное интегрирование.
Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием. Вообще, заметим, что дифференцирование является мощным инструментом проверки результатов интегрирования.
Рассмотрим применение этого метода на примере:
Требуется найти значение интеграла 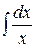 . На основе известной формулы дифференцирования
. На основе известной формулы дифференцирования 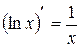 можно сделать вывод, что искомый интеграл равен
можно сделать вывод, что искомый интеграл равен 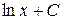 , где С – некоторое постоянное число. Однако, с другой стороны
, где С – некоторое постоянное число. Однако, с другой стороны 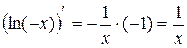 . Таким образом, окончательно можно сделать вывод:
. Таким образом, окончательно можно сделать вывод:
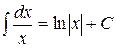
Заметим, что в отличие от дифференцирования, где для нахождения производной использовались четкие приемы и методы, правила нахождения производной, наконец определение производной, для интегрирования такие методы недоступны. Если при нахождении производной мы пользовались, так сказать, конструктивными методами, которые, базируясь на определенных правилах, приводили к результату, то при нахождении первообразной приходится в основном опираться на знания таблиц производных и первообразных.
Что касается метода непосредственного интегрирования, то он применим только для некоторых весьма ограниченных классов функций. Функций, для которых можно с ходу найти первообразную очень мало. Поэтому в большинстве случаев применяются способы, описанные ниже.
Способ подстановки (замены переменных).
Теорема: Если требуется найти интеграл 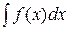 , но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
, но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
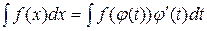
 Примеры решения задач.
Примеры решения задач.
1. Исследовать на экстремум функцию:
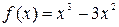
Решение. Имеем 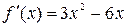 ; тогда из уравнения
; тогда из уравнения 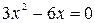 получим:
получим: 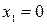 и
и 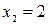 . Составим таблицу:
. Составим таблицу:
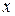
| 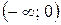
| 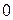
| 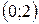
| 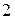
| 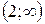
| 
|
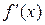
| + | - | + | |||
   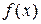
| 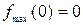
| 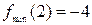
|
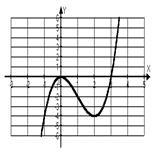
График функции 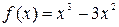 изображен на рисунке внутри таблицы.
изображен на рисунке внутри таблицы.
 2. Вычислить производную функции
2. Вычислить производную функции 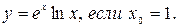
Решение:
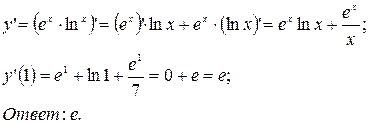
 3. Написать уравнение касательной к графику функции
3. Написать уравнение касательной к графику функции 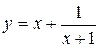 в точке А(0;1).
в точке А(0;1).
Решение: Функция 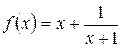 определена, непрерывна и дифференцируема на множестве
определена, непрерывна и дифференцируема на множестве 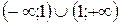 .
.
Выпишем уравнение касательной 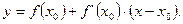
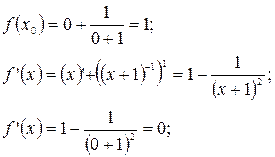
Найдем искомое уравнение касательной: 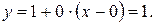
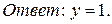
 4. Найти наибольшее и наименьшее значения функции
4. Найти наибольшее и наименьшее значения функции
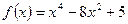 на интервале
на интервале 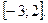
Решение:
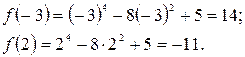
Найдем критические точки функции, т. е. те точки, в которых производная равна нулю:
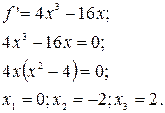

В интервал попадают точки с абсциссами 0; -2; 2. В точке с абсциссой 2 значение функции уже найдено, поэтому найдем ее значения в оставшихся точках:
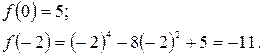

Ответ: 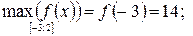
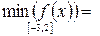
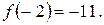
 5. Исследовать функцию
5. Исследовать функцию 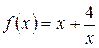 при помощи производной и построить ее график.
при помощи производной и построить ее график.
Решение:
1) Область определения: 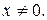
2) Данная функция нечетная, так как 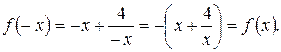 Следовательно, график этой функции симметричен относительно начала координат. Поэтому сначала исследуем эту функцию и построим ее график при
Следовательно, график этой функции симметричен относительно начала координат. Поэтому сначала исследуем эту функцию и построим ее график при 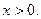
3) 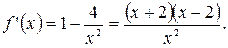
4) На промежутке x>0 функция имеет одну стационарную точку x=2.
5) Производная положительна на промежутке x>2, следовательно, на этом промежутке функция возрастает. На интервале 0<x<2 производная отрицательна, следовательно, на этом интервале функция убывает.
6) Точка x=2 является точкой минимума, так как при переходе через эту точку производная меняет знак с «-» на «+»; 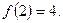
Составим таблицу:
| x | (0;2) | 2 | (2;+ 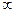 ) )
|
 F(x) F(x)
| 0 | + | |
  F F  (x) (x)
| 
| 4 |
Найдем значения функции еще в двух точках: 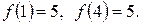
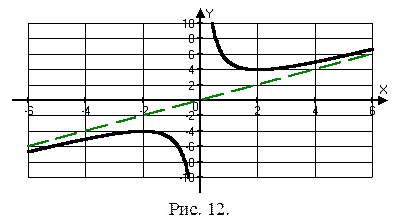
Используя результаты исследования, стоим график функции 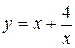 при x>0. График этой функции при x<0 строим с помощью симметрии относительно начала координат (рис.12).
при x>0. График этой функции при x<0 строим с помощью симметрии относительно начала координат (рис.12).
Литература
 2015-01-21
2015-01-21 530
530








