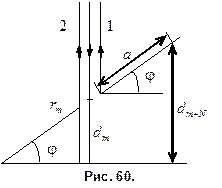 Пример 1. На стеклянный клин нормально к его грани падает монохроматический свет с длиной волны
Пример 1. На стеклянный клин нормально к его грани падает монохроматический свет с длиной волны 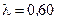 мкм. В возникшей при этом интерференционной картине на отрезке длиной
мкм. В возникшей при этом интерференционной картине на отрезке длиной 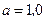 см наблюдается
см наблюдается 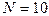 полос. Определить преломляющий угол j клина.
полос. Определить преломляющий угол j клина.
Решение. 1. Параллельный пучок света, падая нормально к грани клина, отражается как от верхней, так и от нижней грани. Эти пучки когерентны и поэтому наблюдается устойчивая картина интерференции. Так как интерференционные полосы наблюдаются при малых углах клина, то отраженные лучи 1 и 2 (см. рис. 60) практически параллельны.
Темные полосы видны на тех участках клина, для которых оптическая разность хода кратна нечетному числу половины длины волны:
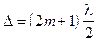 ,
,
где 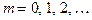
2. Для лучей 1 и 2 оптическая разность хода лучей
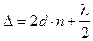 ,
,
где n - показатель преломления стекла, равный 1,5; слагаемое 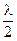 обусловлено изменением фазы луча 1 при отражении от оптически более плотной среды. Приравнивая правые части этих выражений, получаем
обусловлено изменением фазы луча 1 при отражении от оптически более плотной среды. Приравнивая правые части этих выражений, получаем
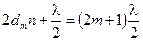 ,
,
отсюда
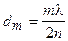 .
.
4. Темной полосе с номером m соответствует толщина клина 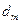 , а темной полосе с номером
, а темной полосе с номером 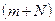 - толщина клина
- толщина клина
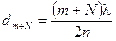 .
.
5. Искомый угол j найдем из соотношения (см. рис. 60):
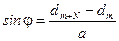 ,
,
6. Из-за малости угла 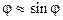 . Отсюда:
. Отсюда:
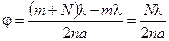 ;
; 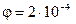 рад.
рад.
В соответствии с общим правилом перевода из радиан в градусы:
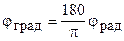 ;
; 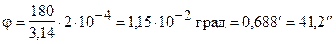 .
.
Ответ: 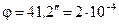 рад.
рад.
 Пример 2. Между стеклянной пластинкой и лежащей на ней плосковыпуклой стеклянной линзой налита жидкость, показатель преломления которой меньше показателя преломления стекла. Радиус
Пример 2. Между стеклянной пластинкой и лежащей на ней плосковыпуклой стеклянной линзой налита жидкость, показатель преломления которой меньше показателя преломления стекла. Радиус 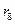 восьмого темного кольца Ньютона при наблюдении в отраженном свете (
восьмого темного кольца Ньютона при наблюдении в отраженном свете (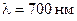 ) равен 2,00 мм. Радиус кривизны выпуклой поверхности линзы равен 1,00 м. Найти показатель преломления n жидкости.
) равен 2,00 мм. Радиус кривизны выпуклой поверхности линзы равен 1,00 м. Найти показатель преломления n жидкости.
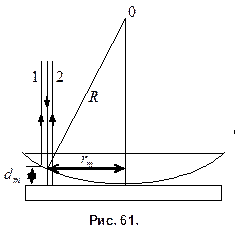
Решение. 1. В отраженном свете кольца Ньютона образуются при наложении лучей, отраженных от нижней поверхности линзы и верхней поверхности плоскопараллельной пластины. Так как радиус кривизны линзы велик, то лучи 1 и 2 (см. рис. 61) практически параллельны.
2. Темные кольца видны при таких толщинах зазора между линзой и пластиной, для которых оптическая разность хода кратна нечетному числу половины длины волны:
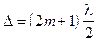 , где
, где 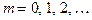
3. Для лучей 1 и 2 оптическая разность хода равна
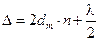 ,
,
где слагаемое 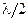 обусловлено изменением фазы луча 2 при отражении от оптически более плотной среды. Приравнивая правые части этих выражений, получаем:
обусловлено изменением фазы луча 2 при отражении от оптически более плотной среды. Приравнивая правые части этих выражений, получаем:
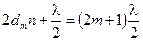 , отсюда
, отсюда 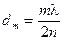 .
.
4. Выразим через радиус темного кольца 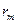 толщину зазора
толщину зазора 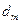 в том месте, где это кольцо наблюдается. Для этого воспользуемся теоремой Пифагора (см. рис. 61):
в том месте, где это кольцо наблюдается. Для этого воспользуемся теоремой Пифагора (см. рис. 61):
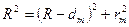 ;
;
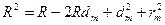 .
.
Слагаемым 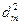 можно пренебречь из-за малости его по сравнению с другими слагаемыми
можно пренебречь из-за малости его по сравнению с другими слагаемыми
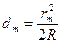 .
.
5. Приравнивая правые части выражений для 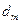 , получаем:
, получаем:
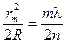 ;
;
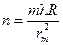 .
.
6. Проведем расчеты показателя преломления жидкости
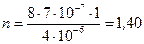 .
.
Ответ: 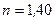
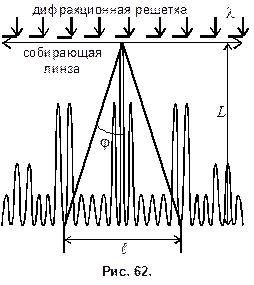 Пример 3. На дифракционную решетку (рис. 62) нормально к её поверхности падает параллельный пучок света с длиной волны
Пример 3. На дифракционную решетку (рис. 62) нормально к её поверхности падает параллельный пучок света с длиной волны 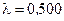 мкм. Помещенная вблизи решетки линза проецирует дифракционную картину на плоский экран, удаленный от линзы на
мкм. Помещенная вблизи решетки линза проецирует дифракционную картину на плоский экран, удаленный от линзы на 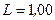 м. Расстояние
м. Расстояние 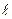 между двумя максимумами интенсивности первого порядка на экране равно 20,2 см. Определить: 1) постоянную d дифракционной решетки; 2) число n штрихов на 1 см; 3) число максимумов, которое дает дифракционная решетка; 4) максимальный угол
между двумя максимумами интенсивности первого порядка на экране равно 20,2 см. Определить: 1) постоянную d дифракционной решетки; 2) число n штрихов на 1 см; 3) число максимумов, которое дает дифракционная решетка; 4) максимальный угол 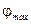 отклонения лучей, соответствующих последнему дифракционному максимуму.
отклонения лучей, соответствующих последнему дифракционному максимуму.
Решение. 1) Постоянная дифракционной решетки d, длина волны l и угол j отклонения лучей, соответствующий максимуму с номером m, связаны соотношением
 .
.
В данном случае 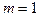 ,
, 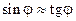 (т.к.
(т.к. 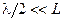 ),
), 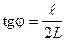 .
.
Поэтому 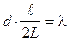 ,
,
откуда 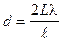 ;
; 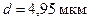 .
.
2) Число штрихов на единице длины связано с d соотношением:
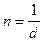 ;
; 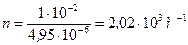 .
.
3) Максимальный угол отклонения лучей решеткой не может превышать 90°, поэтому из условия главных максимумов при 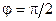 получаем:
получаем:
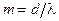 ,
, 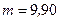 .
.
Число должно быть целым. В то же время, оно не может принять значение, равное 10, т.к. при этом значение sin j будет больше 1, что невозможно. Следовательно,
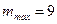 .
.
Общее число максимумов равно 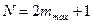 , т.к. вправо и влево от центрального максимума наблюдается по одинаковому числу максимумов:
, т.к. вправо и влево от центрального максимума наблюдается по одинаковому числу максимумов:
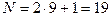 .
.
4) Максимальный угол отклонения лучей 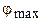 найдем, подставив в условие главных максимумов
найдем, подставив в условие главных максимумов 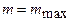 ,
,
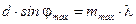 ,
,
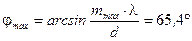 .
.
Ответ: 1) 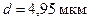 ; 2)
; 2) 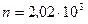 см-1;
см-1;
3) 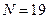 ; 4)
; 4) 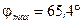 .
.
Пример 4. Как и во сколько раз изменится энергетическая светимость абсолютно черного тела, если максимум энергии излучения переместится с красной границы видимого спектра (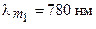 ) на фиолетовую (
) на фиолетовую (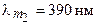 )?
)?
Решение. 1) По аналогии с предыдущей задачей находим выражения для энергетических светимостей в первом и во втором случаях:
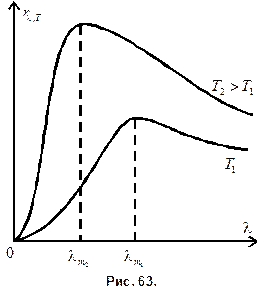
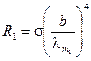 ;
; 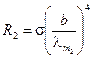 .
.
2) Определим отношение энергетических светимостей:
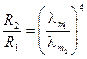 .
.
3) Произведем вычисления:
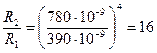 .
.
Видно, что энергетическая светимость увеличится в 16 раз. Этот вывод иллюстрируется рис. 63: при уменьшении 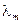 энергетическая светимость R (площадь под кривой
энергетическая светимость R (площадь под кривой 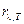 ) возрастает.
) возрастает.
Ответ: 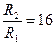 .
.
Пример 5. Определить температуру тонкой абсолютно черной теплопроводящей пластинки, расположенной за пределами земной атмосферы перпендикулярно к лучам Солнца. Радиус орбиты Земли 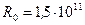 м. Радиус Солнца
м. Радиус Солнца 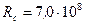 м. Температуру поверхности Солнца принять равной 5,8·103 К.
м. Температуру поверхности Солнца принять равной 5,8·103 К.
Решение. 1. Черная пластинка поглощает падающее излучение, нагревается и сама при этом становится излучателем. В условиях равновесия, т.е. когда 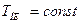 , излучаемая и поглощаемая пластинкой энергии равны друг другу.
, излучаемая и поглощаемая пластинкой энергии равны друг другу.
2. Тонкая теплопроводящая пластинка означает, что вся имеет одинаковую температуру и вся ее поверхность излучает. Пусть площадь пластинки 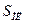 , тогда полная излучающая поверхность 2
, тогда полная излучающая поверхность 2 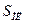 .
.
3. За пределами атмосферы означает, что влияние атмосферы исключено, т.е. нет поглощения энергии атмосферы, нет отдачи энергии пластинкой за счет теплопроводности и конвекции.
4. Поскольку речь идет о полной энергии, следовательно, необходимо пользоваться законом Стефана-Больцмана:
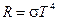 .
.
а) 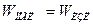 ;
;
б) пластинка излучает со всей поверхности за время 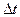 энергию
энергию
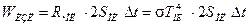 ; (1)
; (1)
в) энергия, получаемая пластинкой за время 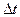 ,
,
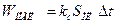 . (2)
. (2)
Здесь 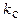 - солнечная постоянная, т.е. энергия, излучаемая Солнцем и падающая ежесекундно на единичную площадку нормально к ее поверхности. Ее можно найти, разделив энергию, излученную Солнцем за время
- солнечная постоянная, т.е. энергия, излучаемая Солнцем и падающая ежесекундно на единичную площадку нормально к ее поверхности. Ее можно найти, разделив энергию, излученную Солнцем за время 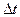 , на площадь поверхности (сферы радиусом
, на площадь поверхности (сферы радиусом 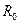 ), через которую она протекает и время
), через которую она протекает и время 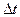 . Используя при этом закон Стефана-Больцмана:
. Используя при этом закон Стефана-Больцмана:
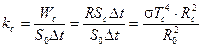 ;
;
г) подставляя в (2) 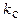 , получим:
, получим:
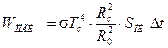 ; (3)
; (3)
д) приравняв правые части (1) и (3) и произведя сокращения, получим
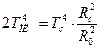 ,
,
а затем найдем температуру пластинки
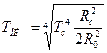 .
.
5. Проведем вычисления
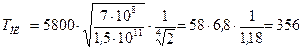 К.
К.
Ответ: 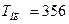 К.
К.
Пример 6. На металлическую пластинку падает монохроматический свет с длиной волны 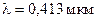 . Поток фотоэлектронов, вырываемых с поверхности металла, полностью задерживается, когда разность потенциалов тормозящего электрического поля достигает
. Поток фотоэлектронов, вырываемых с поверхности металла, полностью задерживается, когда разность потенциалов тормозящего электрического поля достигает 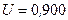 В. Вычислить работу выхода A и красную границу фотоэффекта
В. Вычислить работу выхода A и красную границу фотоэффекта 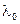 .
.
Решение. 1. Запишем уравнение Эйнштейна для фотоэффекта:
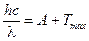 . (1)
. (1)
2. Так как даже самые быстрые электроны задерживаются электрическим полем, пролетев в нем расстояние, соответствующее разности потенциалов U, то
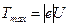 . (2)
. (2)
3. Следовательно,
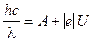 . (3)
. (3)
4. Из (3) найдем работу:
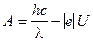 . (4)
. (4)
5. Уравнение Эйнштейна для красной границы:
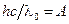 .
.
6. Следовательно,
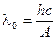 . (5)
. (5)
Подставляя числовые значения в (3) и (5), получаем:
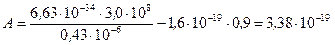 Дж.
Дж.
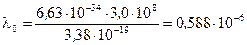 м.
м.
Ответ: 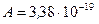 Дж;
Дж; 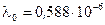 м.
м.
Пример 7. В К¢ -системе покоится стержень, собственная длина которого равна 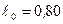 м. Стержень ориентирован относительно направления движения системы под углом
м. Стержень ориентирован относительно направления движения системы под углом 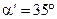 . К ¢-система движется относительно К -системы со скоростью V = 0,70 с в направлении оси 0 х. Найдите в К -системе длину стержня и соответствующий угол a наклона стержня к оси х (рис. 64).
. К ¢-система движется относительно К -системы со скоростью V = 0,70 с в направлении оси 0 х. Найдите в К -системе длину стержня и соответствующий угол a наклона стержня к оси х (рис. 64).
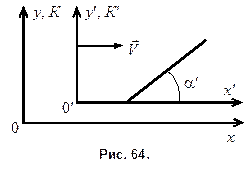 Решение. 1. Найдем проекции стержня на оси координат:
Решение. 1. Найдем проекции стержня на оси координат:
- на ось х:  ; (1)
; (1)
- на ось у: 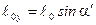 . (2)
. (2)
2. Лоренцево сокращение у стержня наблюдается только в направлении оси х, т.е. проекции стержня в К -системе равны:
- на ось х: 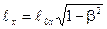 ;
;
- на ось у: 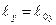 .
.
3. По теореме Пифагора найдем длину стержня в К -системе
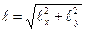 .
.
4. Учитывая (1) и (2) получим
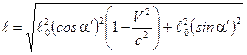 .
.
5. Запишем решение в общем виде
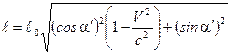 . (3)
. (3)
6. Найдем тангенс угла наклона стержня к направлению движения в К -системе
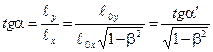 .
.
7. Получим в общем виде решение задачи для угла наклона стержня
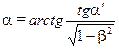 . (4)
. (4)
8. Проведём расчет искомых величин:
- длина стержня в К -системе
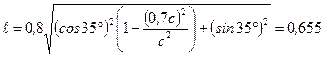 м;
м;
- угол наклона стержня в К -системе
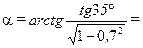 arctg 0,98 = 44,4º.
arctg 0,98 = 44,4º.
Ответ: 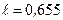 м;
м; 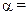 44,4º.
44,4º.
Пример 8. На релятивистскую частицу действует постоянная сила. Найдите зависимость скорости частицы от времени. Считать известной массу т частицы. Рассмотреть случай, когда движение частицы одномерное.
Решение. 1. Запишем второй закон Ньютона в импульсной форме
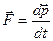 .
.
2. Найдем из него изменение импульса частицы при действии на неё постоянной силы
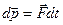 .
.
3. Запишем последнее выражение в проекциях на направление движения
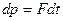 .
.
4. Возьмём интеграл и тем самым найдем импульс частицы к моменту времени t
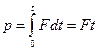 . (1)
. (1)
5. Из релятивистской динамики известно, что импульс равен
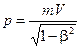 . (2)
. (2)
6. Приравняем правые части уравнений (1) и (2)
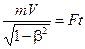 ,
, 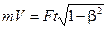 . (3)
. (3)
7. Найдем скорость частицы, решив уравнение (3). Для этого возведём в квадрат левую и правую части равенства (3)
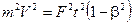 .
.
Раскроем скобки и перенесём в левую часть слагаемые, которые включают в себя скорость частицы
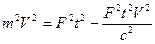 ,
, 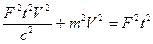 ,
, 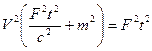 .
.
Найдем скорость частицы
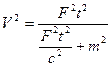 ,
, 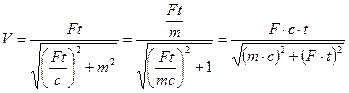 .
.
Ответ: 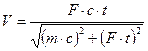 .
.
 2015-01-21
2015-01-21 7513
7513
