Конечной целью выборочного наблюдения является характеристика генеральной совокупности на основе данных, полученных по выборке. При этом исходят из того, что все средние и относительные показатели, полученные по выборке, являются несмещенными и эффективными характеристиками генеральной совокупности.
Выборочные средние и относительные величины распространяются на генеральную совокупность обязательно с учетом предела их возможной ошибки. Приводится выборочный показатель со справкой о пределах ошибки с указанием доверительной вероятности: x̅ ± ∆ x, p ± ∆p. Или же указывают границы значений генеральной характеристики с определенной вероятностью F(t):
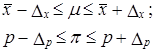
Последняя форма записи является основной.
Иногда требуется указать только один (верхний или нижний) предел характеристики генеральной совокупности. При испытании качества продукции часто нас не интересуют положительные ошибки выборки (качество фактически выше, чем получилось по выборке), беспокоит нижний предел, как в примере, рассмотренном в предыдущем параграфе. В некоторых случаях, напротив, интерес вызывают верхние границы оцениваемых показателей, например при анализе расхода материалов. Так что при характеристике генеральной совокупности всегда указывают неблагоприятный предел.
На основе выборки могут быть получены и значения объемных показателей, т. е. подсчетов для генеральной совокупности. Такой расчет осуществляется двумя способами: путем прямого расчета и способом коэффициентов. Прямой расчет заключается в том, что выборочная средняя или доля умножается на объем генеральной совокупности:
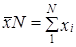 .
.
Так как средняя величина имеет ошибку репрезентативности ± А д то можно считать, что итоговый подсчет в генеральной совокупности находится в пределах
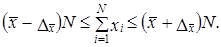 (7.24)
(7.24)
Итоговый подсчет по генеральной совокупности можно получить на основе итогового подсчета по выборке, разделив его на долю отбора единиц совокупности
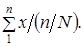
Прежде чем проводить расчет объемных показателей для генеральной совокупности, нужно убедиться, что структура выборки соответствует структуре генеральной совокупности. При наличии значительных смещений в структуре выборки в долях отдельных групп (0,03 и выше) следует применить метод перевзвешивания, г. в. рассчитывать генеральную среднюю на основе выборочных средних по группам и удельного веса этих групп в генеральной совокупности:
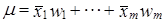 ,
,
где wi = NiN.
При способе коэффициентов также используются не только выборочные данные, но и сведения о генеральной совокупности.
Этот способ основан на связи признаков друг с другом. Например, в результате выборочного обследования семей города получены размер среднедушевого дохода (х̅), средний доход семьи (у̅) и среднее число человек в семье (z̅). Так что x̅ = y̅ / z̅.
Зная численность населения города, требуется рассчитать общую величину денежного дохода населения. Очевидно, это можно сделать, умножив душевой доход на общее число жителей в городе: x̅N. Общий доход можно получить, суммируя доход отдельных семей; численность населения можно получить, суммируя данные о числе членов семей. Тогда
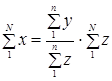 .
.
Средний душевой расход 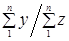 представляет собой коэффициент, подсчитанный по выборке, который связывает две характеристики. Этот коэффициент рассчитывается как отношение двух итоговых подсчетов по выборке:
представляет собой коэффициент, подсчитанный по выборке, который связывает две характеристики. Этот коэффициент рассчитывается как отношение двух итоговых подсчетов по выборке:
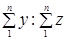 .
.
Следовательно,
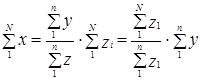 .
.
Последний сомножитель не что иное, как обратная величина доли отбора, рассчитанной по значениям признака z.
Итак, итоговый подсчет по генеральной совокупности может быть получен делением соответствующего итогового подсчета по выборке на долю отбора. При прямом расчете берется доля отбора единиц совокупности, при способе коэффициентов - доля отбора по значению какого-либо признака.
Эффективность способа коэффициентов по сравнению с методом прямого расчета зависит от того, насколько тесно связаны между собой признаки, лежащие в основе расчета коэффициента, т.е. признак, по которому подсчитывается итог, и признак, по которому определяется доля отбора. Эффект проявляется, если коэффициент корреляции между ними больше 0,8.
Способ коэффициентов используется для корректировки данных сплошного наблюдения. Например, перепись скота дала сведения, что поголовье свиней в районе составляет 10 000, в том числе в тех хозяйствах, которые потом были охвачены контрольным обходом, сплошное наблюдение показало число свиней 1100. Контрольный обход дал уточненную цифру: не 1100, а 1107 свиней. Тогда поправочный коэффициент
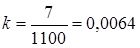 .
.
Отсюда скорректированная численность поголовья свиней во всем районе
N =N¢+∆N; ∆N = kN¢ = ∙10 000 = 64.
N = 10 000 + 64 = 10 064 голов.
 2015-01-21
2015-01-21 320
320








