Вопрос №28

Точечный и интервальный прогноз значения результирующего показателя в условиях ОЛММР

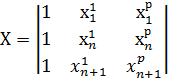
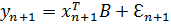
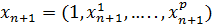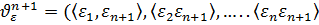^{Т T}

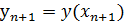=(0,0,…0)

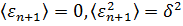
Требуется построить наилучший линейный прогноз для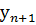

Можно показать что наилучшим будет след. Прогноз

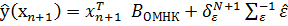
Прогноз будет наилучшим только при отсутствии корреляции между ng w:val="EN-US"/></w:rPr><m:t>n</m:t></m:r><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>+1</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 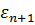и ост. Остатками.

Если автокорреляция будет, то

=

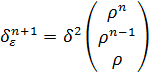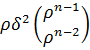
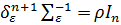, тогда

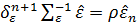
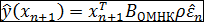
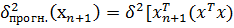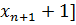
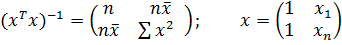
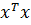^-1

^-1=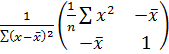

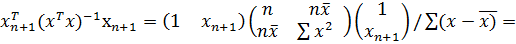
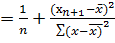
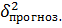
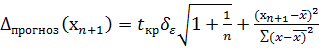
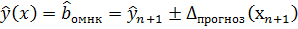
Рассмотрим интервальные прогнозы оценки значений функции регрессии заданной точки.

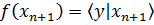
Т.Гаусса – Маркова

Наилучшая точечная оценка определяется значением эмпирической функции регрессии

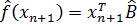
Ср. квадрат ошибки наилучшего точечного прогноза

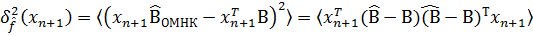
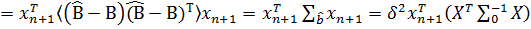^-1x_n+1