2015-02-24
826
Рассмотрим ЛНДУ y” + α1 (x) y’ + α2 (x) y = f (x). Его общим решением является функция y = y* +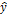 
. Частное решение y* уравнения y” + α1 (x) y’ + α2 (x) y = f (x) можно найти, если известно общее решение 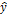соответствующего однородного уравнения y” + α1 (x) y’ + α2 (x) y = 0, методом вариации произвольных постоянных (метод Лагранжа), состоящим в следующем. Пусть 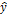= c1y1 (x) + c2y2 (x) – общее решение уравнения y” + α1 (x) y’ + α2 (x) y = 0. Заменим в общем решении постоянные c1 и c2 неизвестными функциями c1 (x) и c2 (x) и подберем их так, чтобы функция y* = c1 (x) · y1 (x) + c2 (x) · y2 (x) была решением уравнения y” + α1 (x) y’ + α2 (x) y = f (x). Найдем производную: (y*)’ = c’1 (x) y1 (x) + c1 (x) y’1 (x) + c’2 (x) y2 (x) + c2 (x) y’2 (x).
Подберем функции c1 (x) и c2 (x) так, чтобы
c’1 (x) · y1 (x) + c’2 (x) · y2 (x) = 0.
Тогда (y*)’ = c1 (x) · y’1 (x) + c2 (x) · y’2 (x),
(y*)” = c’1 (x) · y’1 (x) + c1 (x) · y”1 (x) + c’2 (x) · y’2 (x) + c2 (x) · y”2 (x). Подставляя выражение для y*, (y*)’ и (y*)” в уравнение y” + α1 (x) y’ + α2 (x) y = f (x), получим:
c’1 (x) · y’1 (x) + c1 (x) · y”1 (x) + c’2 (x) · y’2 (x) + c2 (x) · y”2 (x) + α1 (x) [c1 (x) y’1 (x) + c2 (x) y’2 (x)] + α2 (x) [c1 (x) y1 (x) + c2 (x) y2 (x)] = f (x). Поскольку y1 (x) и y2 (x) – решения уравнения y” + α1 (x) y’ + α2 (x) y = 0, то выражения в квадратных скобках равны нулю, а потому c’1 (x) · y’1 (x) + c’2 (x) · y’2 (x) = f (x).
Таким образом, функция y* = c1 (x) · y1 (x) + c2 (x) · y2 (x) будет частным решением y* уравнения y” + α1 (x) y’ + α2 (x) y = f (x), если функции c1 (x) и c2 (x) удовлетворяют системе уравнений:
{c’1 (x) · y1 (x) + c’2 (x) · y2 (x) = 0, (1)
{c’1 (x) · y’1 (x) + c’2 (x) · y’2 (x) = f (x).
Определитель системы | y1 (x) y2 (x) | ≠ 0, т.к. это определитель
| y’1 (x) y’2 (x) |
Вронского для фундаментальной системы частных решений y1 (x) и y2 (x) уравнения y” + α1 (x) y’ + α2 (x) y = 0. Поэтому система (1) имеет единственное решение: c’1 (x) = φ1 (x) и c’2 (x) = φ2 (x), где φ1 (x) и φ2 (x) – некоторые функции от x. Интегрируя эти функции, находим c1 (x) и c2 (x), а затем по формуле y* = c1 (x) · y1 (x) + c2 (x) · y2 (x) составляем частное решение уравнения
y” + α1 (x) y’ + α2 (x) y = f (x).
