Системы дифференциальных уравнений. Основные понятия. Задача Коши для нормальных систем. Линейные системы ДУ. Матричная задача

Системой ДУ называется совокупность ДУ, каждое из которых содержит независимую переменную, искомые функции и их производные.

Общий вид системы ДУ первого порядка, содержащей n искомых функций y₁, y₂, …, y_n, следующий:

{ F₁ (x; y₁ ; y₂ ; …; y_n; y’₁; y’₂; …; y’_n) = 0,

{ ……………………………………………….

{ F_n (x; y₁ ; y₂ ; …; y_n; y’₁; y’₂; …; y’_n) = 0.

Система ДУ первого порядка, разрешенных относительно производной, т.е. система вида

{ dy₁/dx = f₁ (x; y₁; y₂; …; y_n),

{ dy₂/dx = f₂ (x; y₁; y₂; …; y_n), (1)

{…………………………………

{ dy_n/dx = f_n (x; y₁; y₂; …; y_n),

Называется нормальной системой ДУ. При этом предполагается, что число уравнений равно числу искомых функций.

Замечание: во многих случая системы уравнений и уравнения высших порядков можно привести к нормальной системе вида (1).

Решением системы (1) называется совокупность из n функций y₁, y₂, …, y_n, удовлетворяющих каждому из уравнений этой системы.

Начальные условия для системы (1) имеют вид:

y₁ (x₀) = y⁰₁, y₂ (x₀) = y⁰₂, …, y_n (x₀) = y⁰_n.

Задача Коши для системы (1) ставится следующим образом: найти решение системы (1), удовлетворяющее начальным условиям y₁ (x₀) = y⁰₁, y₂ (x₀) = y⁰₂, …, y_n (x₀) = y⁰_n.

Условия существования и единственности решения задачи Коши описывает следующая теорема: если в системе (1) все функции f_i (x; y₁; …, y_n) непрерывны вместе со всеми своими частными производными по y_i в некоторой области D ((n + 1)-мерного пространства), то в каждой точке M₀ (x₀; y⁰₁ ; y⁰₂; …; y⁰_n) этой области существует, и притом единственное, решение y₁ = φ₁ (x), y₂ = φ₂ (x), …, y_n = φ_n (x) системы, удовлетворяющее начальным условиям y₁ (x₀) = y⁰₁, y₂ (x₀) = y⁰₂, …, y_n (x₀) = y⁰_n.

Линейные системы ДУ имеют вид:

dx₁/dt = a₁₁ (t) x₁ + a₁₂ (t) x₂ + … + a_1n (t) x_n + f₁ (t) }

dx₂/dt = a₂₁ (t) x₁ + a₂₂ (t) x₂ + … + a_2n (t) x_n + f₂ (t) } (1)

…………………………………………………….. }

dx_n/dt = a_n1 (t) x₁ + a_n2 (t) x₂ + … + a_nn (t) x_n + f_n (t) }

где f_i (t) – некоторые функции.

dx_i/dt = 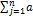_ij (t) x_j + f_i (t), где i = 1,2, …, n.

dX/dt = A · X + F

(dx₁/dt) (x₁ ) (a₁₁ a₁₂ … a_1n) (f₁ (t))

dX/dt = (dx₂/dt), X = (x₂ ), A = (a₂₁ a₂₂ … a_2n), F = (f₂ (t))

(…….) (…) (……………) (……)

(dx_n/dt) (x_n ) (a_n1 a_n2 … a_nn) (f_n (t))

Если все функции a_ij (t) и f_i (t) в системе (1) на некотором отрезке a ≤ t ≤ b непрерывны, то в достаточно малой окрестности точки t₀ a < t₀ < b, координаты которой (t₀, x₁₀, x₂₀, …, x_n0), выполняются условия теоремы Коши о существовании и единственности решения задачи Коши.