Рассмотрим знакоположительный ряд
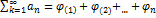 . Если функция φ(k), где k – непрерывная переменная, непрерывная, положительная и убывающая на полуинтервале [1;+∞], то ряд φ(1)+φ(2)+…+φ(n)+…+
. Если функция φ(k), где k – непрерывная переменная, непрерывная, положительная и убывающая на полуинтервале [1;+∞], то ряд φ(1)+φ(2)+…+φ(n)+…+ 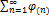 и собственный интеграл
и собственный интеграл 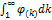 ведут себя одинаково относительно сходимости.
ведут себя одинаково относительно сходимости.
24. Числовые ряды с произвольными членами. Теорема Лейбница для знакочередующихся рядов. Оценка остатка ряда.
Числовой ряд 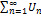 называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов
называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов 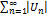 .
.
Знакочередующийся ряд сходится, если (Лейбниц): 1) его члены убывают по абсолютной величине и 2) его абсолютная величина общего члена стремится к нулю, когда n→∞, т.е. 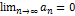 .
.
При этом S ряда удовлетворяет неравенствам: 0< S< U1
Интегральный признак Коши позволяет оценить остаток rn знакоположительного ряда. Из полученного в доказательстве выражения 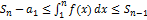 с помощью несложных преобразований получаем:
с помощью несложных преобразований получаем: 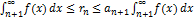 .
.
 2015-02-24
2015-02-24 497
497








