Сглаживание временных рядов с помощью скользящих средних

Альтернативой нахождению некоторой аппроксимирующей функции, которая характеризует ряд целиком, служит метод скользящих средних. В основе этого метода лежит идея о том, что в средних величинах взаимно погашаются случайные отклонения (если дисперсия уровня ряда около среднего (сглаженного) значения a характеризуется величиной s², то разброс среднего из N уровней ряда около того же значения a будет характеризоваться меньшей величиной дисперсии s²/ N, что и означает сглаживание уровней ряда). Первоначальные уровни временного ряда заменяются средними величинами, вычисленными для определенного числа уровней ряда. Полученное значение относится к середине выбранного интервала. Затем интервал сдвигается на одно наблюдение и расчет средней повторяется и т.д. Интервал, на котором вычисляются средние, как бы скользит по ряду.

Сглаживание временного ряда означает представление тренда в данной точке посредством взвешенного среднего значений, наблюдаемых в окрестностях этой точки (активный участок сглаживания). Оно определяется для каждого момента времени, за исключением нескольких первых и нескольких последних точек.

Длину интервала сглаживания 2 m +1 удобно брать нечетной, так как в этом случае полученные значения скользящей средней приходятся на середину интервала.

Сглаженное значение временного ряда y ₁, y ₂,..., y_t,..., y_n в точке t вычисляется по значениям y_{t - m}, y_{t - m +1},..., y_t, y_{t +1},..., y_{t + m} по формуле

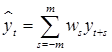, t = m +1,..., n − m, (9.29)

задающей взвешенное среднее наблюдаемых значений y_t в интервале значений t, отстоящих не более чем на m единиц. Полученная таким образом по (9.29) последовательность 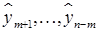называется скользящим средним исходной последовательности y ₁, y ₂,..., y_t,..., y_n.

Определение параметров w_s основано на следующей процедуре. Согласно известной теореме Вейерштрасса любая гладкая функция f_t при самых общих допущениях может быть локально (т.е. в ограниченном интервале изменения ее аргумента t) представлена алгебраическим полиномом подходящей степени p. Таким образом, веса w_s определяются по 2 m +1 членам ряда в результате построения МНК полинома степени p, аппроксимирующего поведение временного ряда. Значение этого полинома в центральной точке (s =0) дает оценку сглаженного значения .

Продемонстрируем процедуру нахождения весов скользящих средних на примере. Пусть необходимо построить наилучшее приближение по пяти точкам (m =2) и нас устраивает локальная аппроксимация квадратичным полиномом = a ₀+ a ₁ t + a ₂ t ² (p =2). Определим веса скользящих средних. Составим систему нормальных уравнений МНК:

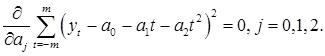
После дифференцирования

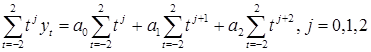или после суммирования

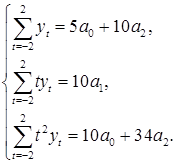
Для t =0 получаем = a ₀ и поэтому, выражая из последней системы a ₀, имеем:

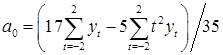= (−3 y_{t -2}+12 y_{t -1}+17 y ₀+12 y_{t +1}−3 y_{t +2})/35,

то есть веса w_s будут равны: 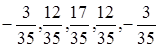, что символически записывается в виде .

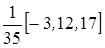Весовые коэффициенты в зависимости от длины интервала сглаживания и порядка полинома представлены в табл. 9.17.

Таблица 9.17

Таблица Каудена для весовых коэффициентов скользящих средних

Длина интервала сглаживания (2 m +1)	Степени полинома
p =2, p =3	p =4, p =5
		−

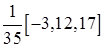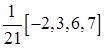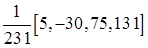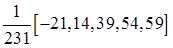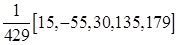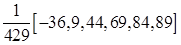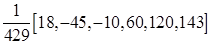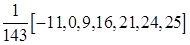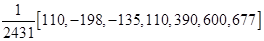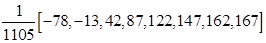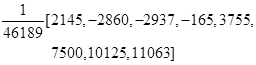Свойства коэффициентов скользящих средних таковы:

− сумма весов равна единице .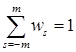

− веса симметричны относительно серединного значения w ₀, т.е. w _{- s} = w_s, s =1,2,…, m. В табл. 9.17 значения w ₀ даны как последние числа в квадратных скобках.

− при одной и той же длине временного интервала веса для полиномов четной степени будут такими же, как и для полиномов степени на единицу большей.

В случае использования полинома первого порядка значение получается как среднее арифметическое из уровней ряда на активном участке сглаживания.

Метод скользящих средних не дает значений тренда для m первых и m последних членов ряда. Особенно неприятно отсутствие значений тренда в конце траектории динамики, поскольку мы хотим экстраполировать ряд. Несмотря на то, что значения тренда в конце не столь устойчивы, как в середине, можно использовать для сглаживания последних m значений ряда полином того же порядка, что и для остальных членов ряда, и получить выражения для весов. Для рассматриваемого выше примера из системы нормальных уравнений получим:

a ₁= =(−2 y_{t −2}− y_{t −1}+ y_{t +1}+2 y_{t +2})/10,

a ₂= 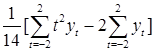=(2 y_{t −2}− y_{t −1}−2 y ₀− y_{t +1}+2 y_{t +2})/14,

затем подставим в уравнение для сглаживающего полинома:

=(−3 y_{t −2}+12 y_{t −1}+17 y ₀+12 y_{t +1}−3 y_{t +2})/35+ t (−2 y_{t −2}− y_{t −1}+ y_{t +1}+2 y_{t +2})/10+

+ t ²(2 y_{t −2}− y_{t −1}−2 y ₀− y_{t +1}+2 y_{t +2})/14,

откуда при t =1, 2 имеем веса скользящих средних для вычисления последнего и предпоследнего значений тренда по пяти (последним) точкам ряда:

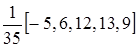и .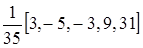

Для выбора конкретных значений длины интервала m и степени полинома p, к сожалению, нет никаких критериев − это зависит от модели представления ряда и цели выделения тренда. При малом числе наблюдений метод скользящих средних часто приводит к искажению тенденции и его надо использовать с осторожностью.

Специфика конкретной задачи может потребовать использования в качестве активного участка четное количество уровней ряда. Например, при анализе среднесуточных колебаний (24 часа), среднемесячных недельных данных (4 недели) и т.п. В этом случае сглаженное значение вычисляется в средней точке скользящего интервала усреднения и попадает посередине между исходными точками наблюдения. Чтобы получить сглаженное значение в точке наблюдения необходимо вычислить значения для двух окаймляющих эту точку промежуточных моментов времени и взять их среднее арифметическое.

После применения скользящих средних ряд сглаженных значений будет более гладким, чем исходный y_t (дисперсия ряда будет меньше дисперсии ряда y_t), однако в нем могут появиться систематические колебания, обусловленные автокоррелированностью его последовательных значений в силу усреднения случайных составляющих. Этот вывод называется эффектом Слуцкого-Юла.