Определение порядка аппроксимирующего полинома с помощью метода последовательных разностей

Для определения порядка аппроксимирующего полинома в указанных выше методах выделения тренда широко используется метод последовательных разностей членов анализируемого временного ряда. Метод основан на математическом факте[3]: если временной ряд y ₁, y ₂,..., y_t,..., y_n содержит в качестве своей неслучайной составляющей алгебраический полином f_t = a ₀+ a ₁ t +...+ a_pt^p порядка р, то переход к последовательным разностям, повторенный р +1 раз (то есть переход к последовательным разностям порядка р +1), исключает неслучайную составляющую (включая константу a ₀), оставляя элементы, выражающиеся только через остаточную случайную компоненту u (t). Алгоритм метода следующий. Последовательно для k =1,2,… вычисляем разности D ^ky_t (t =1,2,…, n − k), а также величины

.

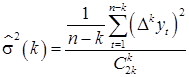Анализируем поведение величины 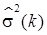в зависимости от k. Величина 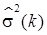будет убывать с ростом k. Начиная с некоторого k = p +1 величина 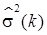стабилизируется, оставаясь приблизительно на одном уровне при дальнейшем росте k. Это значение k = k ₀ и будет давать завышенный на единицу порядок сглаживающего полинома, то есть p = k ₀−1.

При применении метода следует иметь в виду следующее. Сходимость 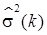не доказывает, что ряд первоначально состоял из полинома плюс случайный остаток. Это означает только то, что он может быть приближенно представлен таким образом.