Прогнозирование периодических колебаний

Во многих временных рядах проявляется сезонный фактор в виде периодических регулярных колебаний, причем период таких колебаний не превышает года и равен кварталу, месяцу или неделе. Пусть выбрана аддитивная модель ряда. Представляется, что невозможно установить полностью объективное правило, разделяющее тренд и сезонность. Однако те или иные методы позволяют приближенно оценить сезонные колебания.

Простейший путь оценки сезонности для ряда y ₁, y ₂,..., y_t,..., y_n с периодом сезонности l (l =12 для ежемесячных данных, l =4 для ежеквартальных данных) заключается в вычислении разности (отношения) между средним по всем одноименным месяцам (кварталам) и средним по всем данным. В результате получаем сезонную компоненту неизменную во времени. Если временной ряд содержит выраженную тенденцию развития, то перед выделением сезонных колебаний сначала должен быть выделен тренд. Обозначим число целых периодов h = n / l, тогда:

.

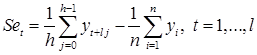Если в последней формуле вычитание заменяется отношением, то получим так называемый индекс сезонности.

Альтернативный метод оценивания сезонной волны состоит в выделении тренда скользящими средними, например, по формуле (m = l /2):

,

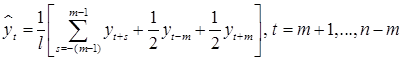и использовании отклонений от сглаженных значений в качестве оценок сезонности:

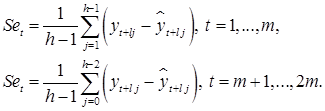(9.30)

Если выбирается мультипликативная модель ряда, то в последней формуле вместо разностей берется отношение.

Разные пределы суммирования объясняются тем, что при использовании скользящей средней с четным значением длины интервала сглаживания m первых и m последних уровней будут потеряны.

Затем полученные значения сезонной компоненты корректируются так, чтобы суммарное воздействие сезонности на динамику было нейтральным. В случае аддитивной модели сумма значений сезонной составляющей для одного периода должна быть равна нулю. Поэтому окончательные оценки сезонности получаются по формуле:

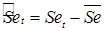, t =1,…, l, (9.31)

где 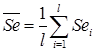. В случае мультипликативной модели: , .

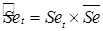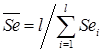Таким образом, построение тренд-сезонной модели в этом случае реализуется в виде следующей последовательности действий.

1. Оценивание сезонной компоненты по формулам (9.30) и (9.31).

2. Переход к временному ряду z_t без сезонной компоненты (десезонализация). В случае аддитивной модели 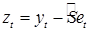, t =1,…, n.

3. Расчет параметров тренда для ряда z_t.

4. Моделирование динамики исходного ряда с учетом трендовой и сезонной составляющих. Оценка точности и адекватности модели.

5. Использование модели для прогнозирования.

Другим способом моделирования сезонной составляющей является использование фиктивных переменных для сезонов:

,

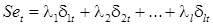где 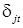− сезонные фиктивные переменные, соответствующие l сезонам, так что 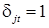для сезона j и 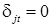иначе, j =1,…, l.

Поскольку в сумме фиктивные переменные 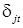дают единицу, то в регрессии с константой будет иметь место линейная зависимость между переменными. Поэтому на коэффициенты накладывается ограничение, например, 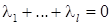. При этом сезонная компонента центрируется, т.е. в среднем влияние сезонной волны на уровень ряда будет нулевым. Тогда:

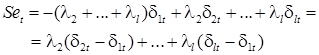
Новые переменные, стоящие в скобках в последнем уравнении будут линейно независимыми и их использование позволяет получить оценки сезонности l₁,…, l _l, которые интерпретируются как отклонения в j -м сезоне от основной динамики ряда на величину l _j.

Если для описания тренда используется полином вида (9.27), то тренд-сезонная модель временного ряда будет иметь вид:

= a ₀+ a ₁ t +...+ a_pt^p + 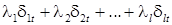+ u_t, (9.32)

где .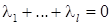

В регрессии (9.32) неизвестные коэффициенты a_i, i =1,…, p и l _j, j =1,…, l находятся МНК, что приводит к выделению трендовой, сезонной и случайной составляющих.

С помощью фиктивных переменных удобно также моделировать выбросы, т.е. аномальные значения временного ряда, которые соответствуют фиксированным моментам времени. Предположим, что в момент времени t ^* произошло некоторое событие (например, дефолт). Тогда, построив фиктивную переменную 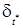=1, если t = t ^* и 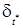=0, если t ≠ t ^*, и включив ее в качестве регрессора, например, в (9.32), сможем учесть в модели соответствующее событие.

Также с помощью фиктивной переменной вида 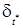=1, если t ≥ t ^* и 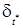=0, если t < t ^* можно учесть в модели структурный сдвиг, произошедший в момент времени t ^*.

На практике часто применяется получивший широкое распространение метод сезонной декомпозиции и корректировки, связанный с деятельностью Бюро переписи США (U.S. Burea of Census). Метод не только позволяет произвести декомпозицию ряда на тренд, сезонность и случайную компоненту, но и учесть различное влияние дней недели, отдельных месяцев, скорректировать экстремальные наблюдения. Временной ряд последовательно подвергается нескольким стадиям обработки, причем итерационно, когда на каждом новом этапе анализа предыдущие оценки пересчитываются. Метод X-11, X-12-ARIMA применяется для квартальных или помесячных данных. Процедура в зависимости от типа требует в качестве исходных данных как минимум 3 полных года и работает при числе наблюдений до 600 (т.е. 50 полных лет при помесячных данных). Рассмотрим процедуру классической сезонной декомпозиции подробно.

1. Предварительная обработка исходных уровней ряда. На этом этапе исключается влияние устойчивых предсказуемых воздействий, например, связанных с календарным фактором:

− эффекты торгового дня: для рядов, описывающих потоки (процессы), корректируется эффект дня недели или только эффект выходных дней, для временных рядов запасов может быть учтен эффект дня месяца, в который наблюдается значение ряда.

− эффект праздничных дней: для временных рядов, описывающих процессы, может быть указано число, определяющее продолжительность времени до праздников, например, если выбрано число 8, то уровень ежедневной активности изменяется за семь дней до праздников и остается на новом уровне до праздников.

2. Временной ряд сглаживается для получения предварительной оценки тренда 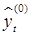. Для этой цели используется скользящая средняя с длиной активного участка 12 для помесячных данных или 4 для квартальных:

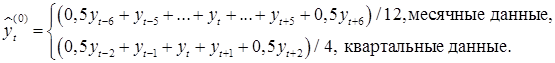
3. Находится отношение соответствующих уровней ряда y_t к уровням 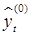для получения предварительной оценки сезонной и случайной компоненты .

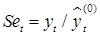4. Полученные значения Se_t усредняются для каждого «сезона» (месяца или квартала) и получают индексы сезонности 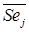, j =1,…, l, затем они корректируются так, чтобы суммарное воздействие сезонности на динамику было нейтральным

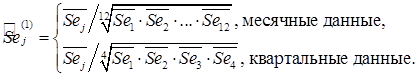
В результате определяется оценка сезонной составляющей 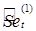. Интерпретация полученных значений − уровни ряда y_t на 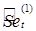процентов выше (ниже) в период t относительно сглаженного временного ряда.

5. Десезонализированный временной ряд получается делением y_t на сезонность : .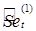

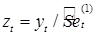6. Пересмотренная оценка тренда 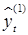получается после сглаживания ряда z_t. Нечетная длина участка сглаживания задается пользователем или выбирается пакетом Eviews автоматически.

7. Случайная компонента 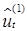получается делением скорректированных на сезонные колебания значений ряда z_t на оценку тренда .

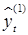В пакетах прикладных программ для чистоты фильтрации повторяются шаги после 6-го, начиная с 3-го. Если используется аддитивная модель временного ряда, то на 3, 5 и 7-м шагах деление заменяется вычитанием, а также на шаге 4 корректировка принимает вид (9.31).

Пример 9.1. Имеются данные об объеме производства продукции предприятия (по месяцам) в сопоставимых ценах, млн. руб.

Таблица 9.18

Месяц	Объём производства	Месяц	Объём производства
Январь	5,1	Июль	5,6
Февраль	5,4	Август	5,9
Март	5,2	Сентябрь	6,1
Апрель	5,3	Октябрь	6,0
Май	5,6	Ноябрь	5,9
Июнь	5,8	Декабрь	6,2

Вычислим среднемесячный выпуск продукции по кварталам, т.е. укрупним интервалы:

Таблица 9.19

Объем производства продукции предприятия (по кварталам) в сопоставимых ценах, млн. руб.

Квартал	Объём производства за квартал	В среднем за месяц
I	15,7	5,23
II	16,7	5,57
III	17,6	5,87
IV	18,1	6,03

После укрупнения интервалов основная тенденция роста производства стала очевидной: 5,23<5,57<5,87<6,03

Пример 9.2. Рассчитаем скользящую среднюю по данным об урожайности зерновых культур.

Таблица 9.20

Исходные данные и результаты расчета скользящей средней, ц/га

Год	Фактический уровень урожайности	Скользящая средняя
Трехлетняя	Пятилетняя
	15,4	-	-
	14,0	(15,4+14,0+17,6)/3=15,7	-
	17,6	(14,0+17,6+15,4)/3=15,7	(15,4+14,0+17,6+15,4+10,9)/5=14,7
	15,4	(17,6+15,4+10,9)/3=14,6	(14,0+17,6+15,4+10,9+17,5)/5=15,1
	10,9	14,6	15,2
	17,5	14,5	17,1
	15,0	17,0	16,8
	18,5	15,9	17,6
	14,2	15,9	-
	14,9	-	-
	åy=153,4

Пример 9.3. Имеются сведения о квартальном товарообороте торговой компании "Дельта" за 20 последних кварталов.

Год / Квартал	Товарооборот	Год / Квартал	Товарооборот	Год / Квартал	Товарооборот	Год / Квартал	Товарооборот
1998/1		1999/2		2000/3		2001/4
1998/2		1999/3		2000/4		2002/1
1998/3		1999/4		2001/1		2002/2
1998/4		2000/1		2001/2		2002/3
1999/1		2000/2		2001/3		2002/4

1). Построим график ряда динамики.

На графике отчетливо видно, что товарооборот изменяется под воздействием сезонных колебаний. Заметен рост в 4 квартале каждого года (соответственно 4, 8, 12, 16 и 20 кварталы), а затем снижение товарооборота в первом квартале каждого года (соответственно 5, 9, 13 и 17 кварталы).

Построение аддитивной модели начнем с выделения сезонной компоненты временного ряда.

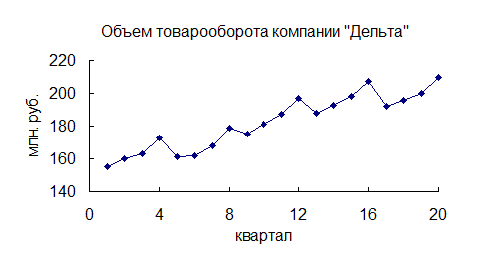
В нашем случае t=4 и h = n /t=20/4=5. Для этого просуммируем уровни ряда по 1-му кварталу по всем пяти годам 155+161+175+188+192=871 и найдем среднее значение 871/5=174,2, и аналогично для остальных кварталов. Получим таблицу 9.21. Среднее значение по всем 20-ти наблюдениям равно 182,25. Вычитая из средних значений по кварталам 182,25 (например, для первого квартала 174,2−182,25=−8,05), получим последнюю строку расчетной таблицы, в которой и содержатся значения сезонной компоненты S_t.

Таблица 9.21

Расчет сезонной компоненты для аддитивной модели

Квартал/Год	I	II	III	IV
Среднее по одноименным кварталам	174,2	178,4	183,2	193,2
St	-8,05	-3,85	0,95	10,95

Устраним сезонную компоненту из исходных уровней ряда и получим z_i = 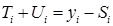в столбце 4 таблицы 9.22.

Далее рассчитаем значения 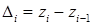представленные в столбце 5 таблицы 9.22. Поскольку первые разности являются примерно одинаковыми (см. столбец 5), считаем, что ряд z имеет линейный тренд. Рассчитаем значения тренда Т. Модель тренда имеет вид 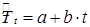. Рассчитаем параметры уравнения тренда. Необходимые предварительные расчеты приведены в таблице 9.22 в столбцах 6-8: столбец 7 получается путем возведения в квадрат значений столбца 6, столбец 8 равен произведению столбца 4 на столбец 6.

Таблица 9.22

Расчет выравненных значений Т и ошибок U в аддитивной модели

i	yi	Si		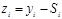Δ i	t	t 2	zt	T	Ui	Ui / yi	| Ui / yi |
		-8,05	163,05	-	-9,5	90,25	-1548,98	158,785	4,265	0,027516	0,027516
		-3,85	163,85	0,8	-8,5	72,25	-1392,73	161,255	2,595	0,016219	0,016219
		0,95	162,05	-1,8	-7,5	56,25	-1215,38	163,725	-1,675	-0,01028	0,010276
		10,95	162,05		-6,5	42,25	-1053,33	166,195	-4,145	-0,02396	0,02396
		-8,05	169,05		-5,5	30,25	-929,78	168,665	0,385	0,002391	0,002391
		-3,85	165,85	-3,2	-4,5	20,25	-746,33	171,135	-5,285	-0,03262	0,032623
		0,95	167,05	1,2	-3,5	12,25	-584,68	173,605	-6,555	-0,03902	0,039018
		10,95	168,05		-2,5	6,25	-420,13	176,075	-8,025	-0,04483	0,044832
		-8,05	183,05		-1,5	2,25	-274,58	178,545	4,505	0,025743	0,025743
		-3,85	184,85	1,8	-0,5	0,25	-92,43	181,015	3,835	0,021188	0,021188
		0,95	186,05	1,2	0,5	0,25	93,03	183,485	2,565	0,013717	0,013717
		10,95	186,05		1,5	2,25	279,08	185,955	0,095	0,000482	0,000482
		-8,05	196,05		2,5	6,25	490,13	188,425	7,625	0,040559	0,040559
		-3,85	196,85	0,8	3,5	12,25	688,98	190,895	5,955	0,030855	0,030855
		0,95	197,05	0,2	4,5	20,25	886,73	193,365	3,685	0,018611	0,018611
		10,95	196,05	-1	5,5	30,25	1078,28	195,835	0,215	0,001039	0,001039
		-8,05	200,05		6,5	42,25	1300,33	198,305	1,745	0,009089	0,009089
		-3,85	199,85	-0,2	7,5	56,25	1498,88	200,775	-0,925	-0,00472	0,004719
		0,95	199,05	-0,8	8,5	72,25	1691,93	203,245	-4,195	-0,02098	0,020975
		10,95	199,05		9,5	90,25	1890,98	205,715	-6,665	-0,03174	0,031738
Сумма								-0,00073	0,415549

Параметры уравнения линейного тренда:

, .

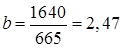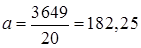Таким образом, уравнение тренда имеет вид:

T =182,25+2,47 t.

Подставляя в уравнение тренда последовательно соответствующие значения t, получим значения тренда для каждого уровня временного ряда (столбец 9 таблицы 5.6), например, для t =−9,5 получим

T (−9,5)=182,25+2,47∙(−9,5)= 158,785.

После выделения тренда остаток U получается как разность между z и T (разность значений в столбцах 4 и 9) и представлен в столбце 10 таблицы 9.22.

Заметим в целях самопроверки, что значения в столбце 2 для y_i должны получаться как сумма значений в столбцах 3, 9 и 10 согласно принятой аддитивной модели.

2). Полученное уравнение временного ряда может быть использовано для краткосрочного прогнозирования. Так, если необходимо спрогнозировать значение товарооборота для 3 квартала 2003 года, то определим t =12,5, так как для 4 квартала 2002 года t =9,5, 1 квартала 2003 года соответственно 10,5, 2 квартала 2003 года 11,5. Подставим значение t в уравнение тренда:

T (12,5)=182,25+2,47∙(12,5)= 213,55.

С учетом того, что сезонная компонента равна для 3-го квартала 0,95, получим окончательно 213,55+0,95 = 214,5.

Таким образом, в третьем квартале 2003 года прогнозируется выручка 214,5 млн. руб.

3). Проверим качество полученной модели.

Рассчитаем среднюю процентную ошибку. Расчет суммы приведен в столбце 11 таблицы 9.22. Таким образом:

MPE =(-0,00073)∙100/20=-0,00367%,

что гораздо меньше 5%.

Рассчитаем среднюю абсолютную процентную ошибку. Расчет суммы приведен в столбце 12 таблицы 9.22. Таким образом:

MАPE =(0,415549)∙100/20=2,08%,

и поскольку MAPE <10%, то модель подогнана с высокой точностью.

Средняя ошибка суть ME =10/20 = 0,5.

Пример 9.4. Имеются поквартальные данные об объеме экспорта одной из областей РФ за 5 лет (млн. долл.).

Год / Квартал	Объем экспорта, млн.долл.	Год / Квартал	Объемэкспорта, млн.долл.	Год / Квартал	Объем экспорта, млн.долл.	Год / Квартал	Объем экспорта, млн.долл.
1998/1	19,3	1999/2	15,8	2000/3	20,3	2001/4	25,4
1998/2	12,3	1999/3	17,2	2000/4	22,3	2002/1	31,8
1998/3	13,2	1999/4	19,9	2001/1	29,7	2002/2	23,9
1998/4	15,6	2000/1	26,3	2001/2	21,1	2002/3	25,8
1999/1	21,5	2000/2	19,1	2001/3	23,7	2002/4	27,4

Рассмотрим построение мультипликативной модели на примере.

1). Проведем выравнивание ряда методом скользящей средней. Для этого просуммируем уровни ряда по 4 кварталам последовательно. Далее разделим полученные суммы на 4 и найдем скользящие средние, уже не содержащие сезонной компоненты. Найдем центрированные скользящие средние, для чего вычислим средние значения из двух последовательных скользящих средних. Вычислим оценки сезонной компоненты как частное от деления фактического уровня экспорта на центрированные скользящие средние.

Таблица 9.23

Расчет оценок сезонной компоненты

Квартал	Объем продаж, тыс.шт.	Итого за 4 квартала	Скользящая средняя за 4 квартала	Центрированная скользящая средняя	Оценка сезонной компоненты
	19,3
	12,3
		60,4	15,1
	13,2			15,375	0,858537
		62,6	15,65
	15,6			16,0875	0,969697
		66,1	16,525
	21,5			17,025	1,262849
		70,1	17,525
	15,8			18,0625	0,87474
		74,4	18,6
	17,2			19,2	0,895833
		79,2	19,8
	19,9			20,2125	0,984539
		82,5	20,625
	26,3			21,0125	1,251636
		85,6	21,4
	19,1			21,7	0,880184
	20,3			22,425	0,90524
		91,4	22,85
	22,3			23,1	0,965368
		93,4	23,35
	29,7			23,775	1,249211
		96,8	24,2
	21,1			24,5875	0,85816
		99,9	24,975
	23,7			25,2375	0,939079
			25,5
	25,4			25,85	0,982592
		104,8	26,2
	31,8			26,4625	1,201701
		106,9	26,725
	23,9			26,975	0,886006
		108,9	27,225
	25,8
	27,4

Используем полученные оценки сезонности для расчета сезонной компоненты S. Для этого найдем средние квартальные оценки сезонной компоненты, используя данные всех кварталов.

Таблица 9.24

Расчет значений сезонной компоненты

Показатели	Год	Квартал
	-	-	0,8585	0,9696
	1,2628	0,8747	0,8958	0,9845
	1,2516	0,8801	0,9052	0,9653
	1,2492	0,8581	0,9390	0,9825
	1,2017	0,8860	-	-
Итого за квартал	4,9653	3,4990	3,5986	3,9021
Средняя оценка сезонной компоненты для квартала	1,2413	0,8747	0,8996	0,9755
Скорректированная оценка сезонной компоненты	1,2440	0,876	0,9016	0,9776

Заметим, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле. В нашем примере, цикл – год, в котором соответственно 4 квартала. Поэтому окончательный вариант сезонной компоненты будет получен корректировкой, заключающейся в умножении средней оценки сезонной компоненты для квартала на коэффициент k:

k =4/(1,2413+0,8747+0,8996+0,9755)=4/3,9913=1,0021.

Полученные таким образом значения были занесены в табл. 9.24 (строка 3).

2). Устраним сезонную компоненту из исходных уровней ряда и получим выравненные данные T × U = y_i / S (столбец 4, табл. 9.25).

Таблица 9.25

Расчет выравненных значений Т и ошибок U в мультипликативной модели

t	yi	S	T × U = yi / S	T	Т × S	U= yi /(T × S)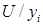
	19,3	1,244	15,5139	14,2959	17,7841	1,0852	0,0562
	12,3	0,8766	14,0303	15,069	13,2095	0,9311	0,0757
	13,2	0,9016	14,6402	15,8421	14,2832	0,9242	0,0700
	15,6	0,9776	15,9563	16,6151	16,2429	0,9604	0,0616
	21,5	1,244	17,2823	17,3882	21,6309	0,9939	0,0462
	15,8	0,8766	18,0227	18,1613	15,9202	0,9925	0,0628
	17,2	0,9016	19,0767	18,9344	17,0713	1,0075	0,0586
	19,9	0,9776	20,3546	19,7074	19,266	1,0329	0,0519
	26,3	1,244	21,1407	20,4805	25,4777	1,0323	0,0392
	19,1	0,8766	21,7869	21,2536	18,6309	1,0252	0,0537
	20,3	0,9016	22,5149	22,0266	19,8592	1,0222	0,0504
	22,3	0,9776	22,8094	22,7997	22,289	1,0005	0,0449
	29,7	1,244	23,8738	23,5728	29,3246	1,0128	0,0341
	21,1	0,8766	24,0683	24,3459	21,3416	0,9887	0,0469
	23,7	0,9016	26,2859	25,1189	22,6472	1,0465	0,0442
	25,4	0,9776	25,9802	25,892	25,312	1,0035	0,0395
	31,8	1,244	25,5618	26,6651	33,1714	0,9587	0,0301
	23,9	0,8766	27,2622	27,4381	24,0522	0,9937	0,0416
	25,8	0,9016	28,615	28,2112	25,4352	1,0143	0,0393
	27,4	0,9776	28,0259	28,9843	28,3351	0,967	0,0353
Cумма						19,993	0,982

3).Определим компоненту Т. Для этого проведем аналитическое выравнивание ряда (Т × U) с помощью линейного тренда. Имеем линейный тренд вида:

T = 13,5229+0,7730 t.

Стандартная ошибка коэффициента регрессии 0,735.

Подставляя в уравнение тренда последовательно t= 1,…,20, получим значения тренда для каждого уровня временного ряда (столбец 5, табл. 9.25).

4). Найдем значения уровней ряда, полученные по мультипликативной модели как (T × S) (столбец 6, табл. 9.25).

5). Проверим качество модели. Рассчитаем необходимые показатели. Необходимые предварительные расчеты проведем в столбцах 7,8. В данном конкретном случае средняя абсолютная процентная ошибка (MAPE) будет равна средней процентной ошибке(MPE):

MPE=MAPE =(0,982)∙100/20=4,91%,

что меньше 5%, а значит модель подогнана с высокой точностью.

Средняя ошибка ME с учетом суммы в столбце 7 таблицы 9.25, суть ME =19,993/20 = 0,9997.

6). Спрогнозируем объем экспорта в 3 квартале 2003 года. Прогнозное значение временного ряда в мультипликативной модели есть произведение трендовой и сезонной компонент. Трендовая компонента рассчитывается как T =13,5229+0,7730 ^. 23=31,3019. Значения сезонной компоненты третьего квартала равны 0,9016. Таким образом, общее прогнозное значение объема экспорта будет получено как 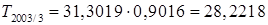млн. $.

Контрольные вопросы к главе 9

1. Что такое ряды динамики и из роль в статистическом анализе?

2. Укажите виды рядов динамики.

3. Чем объясняется выбор формулы для нахождения среднего уровня динамического ряда?

4. Какие показатели рассчитываются для характеристики изменений уровней ряда динамики?

5. Как рассчитывается средний темп (коэффициент) роста и прироста?

6. Укажите приемы, применяемые для преобразования временных рядов.

7. Каким образом временные ряды приводят к одному основанию?

8. Чем вызвана необходимость смыкания временных рядов?

9. Назовите методы анализа основной тенденции развития в рядах динамики.

10. На чем основан метод укрупнения интервалов?

11. Чем вызвана необходимость аналитического выравнивания рядов?

12. Какие методы выделения тренда вы знаете? Когда они применяются? Каковы их достоинства и недостатки?

13. Как определить порядок аппроксимирующего полинома при выделении неслучайной составляющей?

14. В чем суть метода кривых роста? Каковы его недостатки?

15. Какие виды кривых роста вы знаете и каковы способы подбора кривой.

16. Какие вы знаете методы оценки адекватности и точности прогноза? Когда используется каждый из этих методов?

17. В чем суть метода скользящих средних? Каковы его недостатки?

18. В чем суть эффекта Слуцкого-Юла?

19. Каковы достоинства и недостатки методов оценки качества прогноза?

20. Какие требования предъявляются к остаткам адекватной модели временного ряда?

21. Какие показатели качества модели и прогноза рассчитываются в статистических пакетах прикладных программ?

22. Как оценивается сезонность в аддитивной и мультипликативной моделях?

23. Как с помощью фиктивных переменных оценить сезонные колебания, структурные сдвиги?

24. В чем отличие сезонной компоненты временного ряда от циклической?

25. Как построить прогноз сезонной компоненты временного ряда?

Тесты для самопроверки к главе 9

1.	Уровнем динамического ряда является…:
	1.	значения показателя за определенный период времени или на определенную дату
	2.	значения варьирующего признака в совокупности
	3.	обобщающая характеристика изучаемого признака в совокупности
	4.	совокупность значений показателя за определенный период времени
2.	С точки зрения теории статистики ряд динамики включает следующие составные элементы …(выберите несколько вариантов ответа)
	1.	значения изучаемого показателя
	2.	интервалы изменения признака
	3.	частоты
	4.	показатели времени
3.	Средний уровень интервального ряда динамики определяется как средняя …
	1.	геометрическая
	2.	квадратическая
	3.	арифметическая
	4.	хронологическая
4.	Средний уровень моментного ряда динамики определяется как средняя …
	1.	геометрическая
	2.	квадратическая
	3.	арифметическая
	4.	хронологическая
5.	Абсолютный прирост исчисляется как
	1.	отношение уровней ряда
	2.	сумма уровней ряда
	3.	разность уровней ряда
	4.	разность последнего и первого наблюдений
6.	Показатель ряда динамики, характеризующий абсолютный прирост в относительных величинах, есть
	1.	абсолютный прирост цепной
	2.	темп роста базисный
	3.	темп прироста
	4.	темп прироста
7.	Для выявления тренда используют (выберите несколько вариантов ответа)
	1.	усреднение интервалов
	2.	метод скользящей средней
	3.	смыкание рядов
	4.	расчет коэффициентов роста
8.	Индекс сезонности можно рассчитать как
	1.	отношение фактического уровня ряда к среднему за год
	2.	отношение среднего уровня ряда за сезон к среднему за год
	3.	отношение фактического уровня ряда к выравненному за тот же период
	4.	отношение суммы уровней ряда за сезон к сумме уровней за год
9.	Зависимость себестоимости продукции (т.р./шт.) от объёма выпуска (шт.) имеет вид гиперболы: 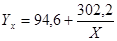. Пропорциональные объёму выпуска издержки составляют (в т.р./шт.):
	1.	94,6
	2.	302,2
	3.
	4.	302200.
	Показатель растет ежегодно на 2 единицы. Чему будет равен коэффициент линейного тренда ряда динамики этого показателя:
	1.	0,5
	2.
	3.
	4.