Некоторые достаточные признаки сходимости рядов с положительными членами

1. Признак сравнения. Рассмотрим два числовых ряда с положительными членам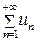и и 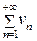. Если при всех 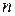, начиная с некоторого номера, 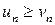, то из сходимости ряда 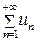следует сходимость ряда 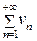. Наоборот, из расходимости ряда 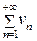следует расходимость ряда .

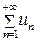При использовании признака сравнения нужно иметь эталонный ряд, про сходимость которого известно заранее. В качестве таких рядов чаще всего берут обобщенный гармонический ряд 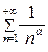, который сходится при 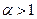и расходится при 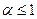, или геометрический ряд 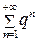, который сходится при 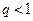и расходится при .

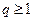2. Признак сходимости Даламбера. Пусть для ряда с положительными членами 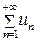существует предел 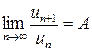. Тогда: если 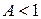, то ряд сходится; если 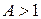, то ряд расходится. При 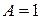признак Даламбера ответа не дает: ряд может, как сходиться, так и расходиться.

3. П ризнаки сходимости знакопеременных рядов

Если члены числового ряда имеют разные знаки, то ряд называется знакопеременным. Частным случаем знакопеременного ряда является знакочередующийся ряд вида 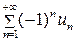, где .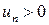

Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд из абсолютных величин членов ряда, т.е. ряд вида 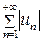. Если ряд из абсолютных величин расходится, а сам ряд сходится, то его называют условно сходящимся. Исследование знакопеременного ряда начинают с исследования на сходимость ряда из абсолютных величин методами, которые применяются для рядов с положительными членами. Если такой ряд сходится, то получен ответ: ряд сходится абсолютно.

Если ряд из абсолютных величин расходится, то для знакочередующегося ряда можно применить признак Лейбница: если члены ряда 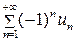стремятся к нулю, монотонно убывая, то ряд сходится, по крайней мере, условно.