Пусть функция 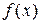 определена в некоторой окрестности точки
определена в некоторой окрестности точки 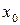 и имеет в этой точке производные всех порядков. Ряд вида:
и имеет в этой точке производные всех порядков. Ряд вида: 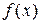 =
= 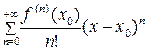 ,
,
называется рядом Тейлора для функции 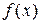 в точке
в точке 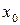 . При
. При 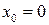 такой ряд называют также рядом Маклорена. Функция
такой ряд называют также рядом Маклорена. Функция 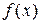 может быть разложена в степенной ряд на интервале
может быть разложена в степенной ряд на интервале 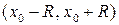 , если существует степенной ряд, сходящийся к
, если существует степенной ряд, сходящийся к 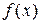 на этом интервале. Если функция раскладывается в степенной ряд в некоторой окрестности точки
на этом интервале. Если функция раскладывается в степенной ряд в некоторой окрестности точки 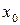 , то это ряд Тейлора. Приведем разложения в ряд Тейлора для некоторых элементарных функций:
, то это ряд Тейлора. Приведем разложения в ряд Тейлора для некоторых элементарных функций:
1) 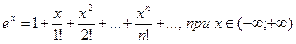 ;
;
2) 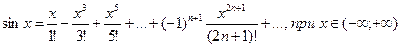 ;
;
3) 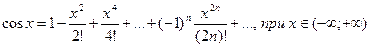 .
.
 2015-02-24
2015-02-24 477
477








