Алгебраическая проблема собственных значений

Вектор 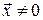- собственный вектор матрицы A:

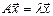(1)

l - собственное значение матрицы A, или СЛАУ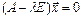

Необходимо и достаточно:

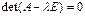(2)

Характеристический многочлен

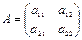
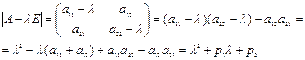
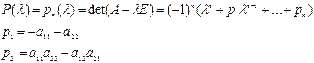
Свойство 1:

Если - собственная пара матрицы А, a¹0 – число, то 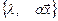является собственной парой А.

Из (1) 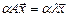или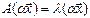

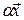- собственный вектор,

l - собственное число А.

Свойство 2:

Пусть 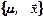- собственная пара матрицы 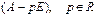, тогда 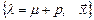- собственная пара матрицы А.

Из (1):

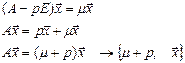
собственная пара для А.

Свойство 3:

Пусть 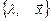- собственная пара матрицы А, тогда 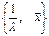- собственная пара для матрицы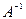

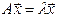
Умножим слева на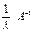

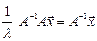
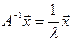
Свойство 4:

Собственными числами диагональных и треугольных матриц являются .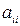

Из (2) имеем:

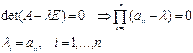
Степенной метод (определение наибольших по модулю l и ).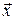

Пусть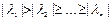

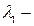собственное число матрицы А,

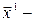собственный вектор, соответствующий .

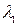Возьмем произвольный вектор :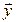

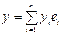
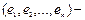базис.

Итерации вектора:

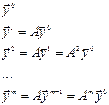
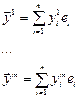
координаты вектора в базисе .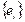

Собственные вектора 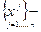образуют базис (линейно–независимы)

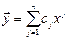- разложение по базису из собственных векторов.

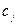- const.

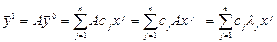
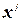- собственный вектор матрицы А.

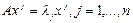
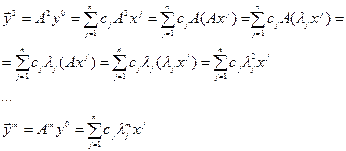(3)

Разложение по базису 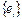собственных векторов .

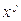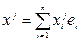(4)

(4) (4) (3)

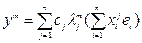
или

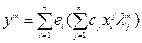
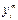- координаты в базисе .

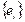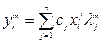
Аналогично:

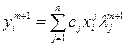
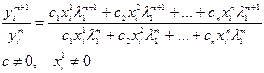
Выбор 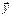и .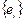

Делим на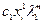

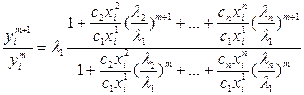
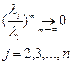
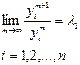
или

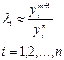
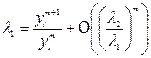
m - достаточно большое.

Вектор 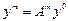является собственным вектором А.

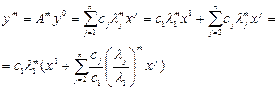
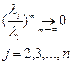
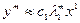
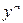отличается от 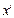на константу a.

Итак:

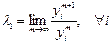
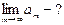
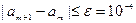
e - задано.

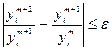
m -?

По i среднее арифметическое:

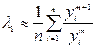
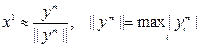
Применение степенного метода для нахождения наименьшего по модулю собственного числа 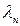знакоопределенной матрицы А, когда 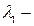уже найдено.

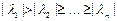
Для этого находим наибольшее по модулю собственное число 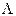- матрицы .

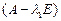Тогда соответствующий 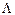собственный вектор и число 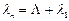будут образовывать искомую собственную пару.

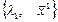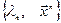Действительно пусть и - собственные пары матрицы