Рассмотрим задачу, возникающую при изучении каких-либо закономерностей на основе наблюдения или экспериментов. Характерной особенностью таких задач является то, что исходный материал – заведомо приближенный, в силу неточности измерительных приборов, неповторимости условий наблюдений, случайных ошибок и пр.
Предположим, что между независимой переменной x и зависимой переменной y имеется некая неизвестная функциональная связь
y = f(x).
Эта связь отображается таблицей
| x | x0 | x1 | … | xn |
| y | y0 | y1 | … | yn |
приближенных значений yi» f(xi), получаемых в ходе наблюдений или экспериментов.
Требуется дать приближенное аналитическое описание этой связи, т.е. подобрать функцию j(x) такую, которая аппроксимировала бы на отрезке [x0, xn] заданную отдельными приближенными значениями yi функцию f(x).
Для решения этой задачи заведомо неудачным является интерполяционный подход хотя бы потому, что функция j(x) такая, что
j(xi) = yi при всех iÎ {0,1,…,n},
будет мало похожа на искомую f(x), поскольку в ней отразятся все ошибки экспериментальных данных.
Это заставляет отказаться от идеи интерполяции и находить функцию j(x) такую, чтобы она хорошо отражала в среднем зависимость между x и y.
А именно, из каких-либо соображений (аналитических, графических или иных) аппроксимирующая функция j(x) берется из определенного m - параметрического семейства функций, и ее параметры подбираются так, чтобы сумма квадратов отклонений значений j(xi) от заданных приближенных значений yi была минимальной.
Такая функция (т.е. при таком оптимальном наборе параметров) будет наилучшей аппроксимацией f(x) среди функций выбранного семейства в смысле метода наименьших квадратов.
Ясно, что число данных приближенных значений yi в таблице должно быть не меньшим, чем число параметров в подбираемой зависимости j(x); как правило, считается, что n>>m.
Итак, согласно МНК, задаем семейство
Y=j(x, a1, a2,…, am)
И ищем значения параметров a1, a2,…, am (где m£ n), решая экстремальную задачу (задачу на экстремум функции)
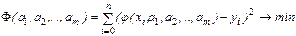
Оптимальный набор параметров, a*1, a*2,…, a*m может быть найден из необходимых условий гладкого экстремума, т.е. в результате приравнивания к нулю частных производных функции 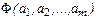 , взятых по каждому из ее аргументов.
, взятых по каждому из ее аргументов.
Получаем следующую систему уравнений относительно
неизвестных a1, a2,…,am
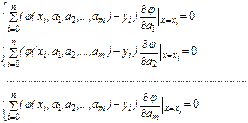 (1)
(1)
Эти условия экстремума в силу специфики функции являются и достаточными условиями ее минимума.
В зависимости от характера табличных данных, (изучаемых с помощью графика), часто используют следующие
двухпараметрические семейства функций:
 y=ax+b, y=a+blnx, y=ax b, y=1/(ax+b)
y=ax+b, y=a+blnx, y=ax b, y=1/(ax+b)
Трехпараметрические семейства: Y=ax2+bx+c, y=axb+c, y=aebx+c
При изучении периодических явлений применяют тригонометрические функции.
Рассмотрим, к чему сводится процесс построения наилучших среднеквадратических приближений в одном конкретном, но общем, случае, когда аппроксимирующая f(x) функция j(x) представляет собой линейную комбинацию нескольких других, вообще говоря, более простых (базисных) функций.
Пусть 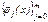 - некоторая заданная на [a, b] система линейно независимых функций.
- некоторая заданная на [a, b] система линейно независимых функций.
Обобщенным многочленом будем называть функцию
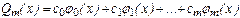 (3)
(3)
Где сi - произвольные вещественные числа (коэффициенты обобщенного многочлена).
Поскольку функции jj(x) считаются заданными, построение многочлена наилучшего приближения для данной функции f(x) сводится к нахождению оптимального набора c*0, c*1,,c*m коэффициентов Qm(x) в (3) на основе метода наименьших квадратов, т.е. к решению задачи минимизации:
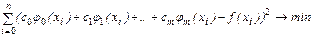
В дискретном случае необходимые и достаточные условия экстремума выражаются системой
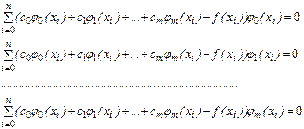 (4)
(4)
После элементарных преобразований она может быть переписана в терминах скалярных произведений:
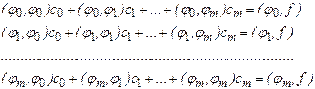 (4)
(4)
Если сеточные функции jj(xi) образуют систему линейно независимых элементов пространства Rn+1[a, b], то полученная симметричная линейная алгебраическая система (4), называемая нормальной системой МНК, имеет заведомо отличный от нуля определитель, и значит, однозначно разрешима.
Следовательно, при заданном базисе 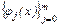 путем решения системы (4) можно найти единственный обобщенный многочлен
путем решения системы (4) можно найти единственный обобщенный многочлен
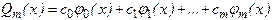
такой, что f(x)» Qm(x) при x Î[a, b} с наименьшей квадратичной ошибкой
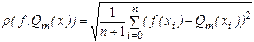
 2015-02-24
2015-02-24 1053
1053
