2015-02-24
406
Оценим остаточный член, т.е. разность Rn-(x)=f(x)-Ln(x)
Потребуем, чтобы в области [ a, b] изменения x функция f(x) была дифференцируема (n+1) раз, т.е. f’(x),…, f(n+1) (x).
Ясно, что в узлах интерполяции эта погрешность Rn(x)=0.
Оценим ее в любой точке x Î [ a, b].
Рассмотрим вспомогательную функцию
u(x)=f(x)-Ln(x)-kПn+1(x), где
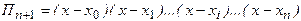
- K - постоянный коэффициент, который выберем ниже.
U(x) имеет (n+1) нуль (корень) в т. x0, x1, …, xn.
Подберем k так, чтобы u(x) имела n+2 корень в любой фиксированной точке x’ отрезка [ a, b ], не совпадающий с узлами интерполирования. Т.е. u(x’)=0.
Положим f(x’)=Ln(x’)-kПn+1(x’).
Тогда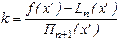 
При этом значении k функция u(x) будет иметь (n+2) корня в
узлах x’,x0, x1, …, xn.
Применяя теорему Ролля на каждом из отрезков [x0, x1],[x1, x2],…,
[xi, x’], [x’, xi],…,[xn-1, xn] убеждаемся, что производная u’(x) имеет не менее (n+1) корня на [ a, b].
U’’(x) – n раз обращается в нуль на [ a, b].
………………………………………………
U (n+1)(x) - имеет 1 корень
Пусть U (n+1)(x)=0, xÎ[ a, b].
Так как Ln(n+1)(x)=0 и Пn+1(n+1)(x)=(n+1)!, имеем
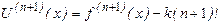
При x=x, получаем
® 
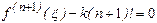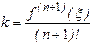
Т.о. Rn(x)=f(x)-Ln(x)=?
В силу того, что U(x’)=0, имеем
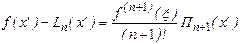
Т.к. x’ - произвольно, то
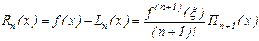, где xÎ[ a, b].
Обозначим через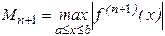 
Получим формулу для погрешности интерполяционной формулы Лагранжа
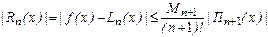
Если f(x) - многочлен n -ой степени, то f(x)=Ln(x) и Rn(x)=0 в силу единственности.
Пример:
С какой точностью можно вычислить Ö115 с помощью Ln(x) для y=Öx, если x0=100, x1=121, x2=144.
Y’=0.5x-1/2, y’’=-1/4x-3/2, y’’’=3/8x-5/2. M3=max|y’’|=3/8 1/Ö1005=3/2 10-5.
|R2|£3/8 10-5 1/3! |(115-100)(1150121)(115-144)|=1.6 10-3.
