Схема Лакса

Разностную схему Эйлера можно сделать устойчивой, если заменить

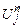на пространственное среднее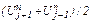

В результате получим широко известную схему Лакса:

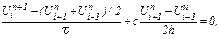
Это явная одношаговая схема с погрешность аппроксимации O(t, h²/t ).

Множитель перехода равен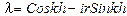

Схема устойчива при 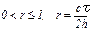– число Куранта

Отметим, что эта схема не всегда обладает условием согласованности, так как 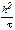может не стремится к нулю при 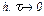. Однако если число Куранта 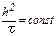, то при 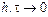условие согласованности выполняется.

Согласованной называется разностная схема, аппроксимирующая данное уравнение в частных производных, т. е. погрешность аппроксимации (разность между дифференциальным уравнением и его конечно-разностным аналогом) стремится к нулю при измельчении сетки.