2015-02-24
330
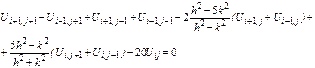
Погрешность аппроксимации разностной схемы О(h4+k4), на квадратной сетке О(h6),
|
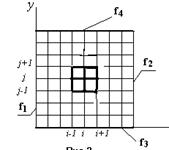
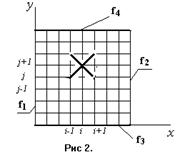
3. Так как оператор Лапласа инвариантен относительно поворота системы координат, то на квадратной сетке можно вместо использовать диагональные узлы. Шаг сетки увеличится до Ö2 h.
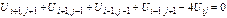
Погрешность аппроксимации разностной схемы О (h2).
Для определения величин Ui,j требуется решить систему линейных алгебраических уравнений Методы решения разделяются на прямые и итерационные.
Прямые методы: Метод Гаусса и его модификации, прогонки.
Итерационные методы: метод итераций, метод Зейделя
Итерационный метод Зейделя:
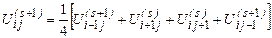
где верхний индекс s - номер итерации. При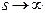 
последовательность
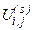сходится к точному решению системы.
В качестве условия окончания итерационного процесса можно принять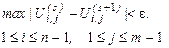 
.
Погрешность приближенного решения, получаемого конечно- разностным методом, складывается из двух погрешностей: погрешности аппроксимации дифференциального уравнения разностным и погрешности итерационного процесса.
|
|
|
