Пусть 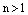 – натуральное число. По формуле корней из комплексногочисла, существует ровно n корней из комплексного числа
– натуральное число. По формуле корней из комплексногочисла, существует ровно n корней из комплексного числа  . Для вычисления этих корней запишем единицу в тригонометрическойформе:
. Для вычисления этих корней запишем единицу в тригонометрическойформе:
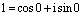 , т.е.
, т.е. 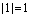 ,
, 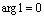 .
.
Обозначим все множество корней через 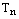 . По формуле корней получаем:
. По формуле корней получаем:
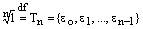 , (6)
, (6)
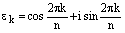 ,
, 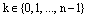 . (7)
. (7)
В частности, 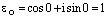 ,
,
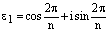 . (8)
. (8)
Заметим, что 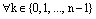 верна формула:
верна формула:
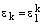 . (9)
. (9)
Действительно, равенство (9) сразу же получается по формуле Муавра:
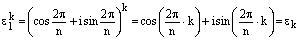 .
.
Теперь мы все множество корней 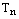 из 1 можем записать так:
из 1 можем записать так:
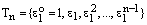 (10)
(10)
Теорема. Множество всех корней из 1 является коммутативной группой.
Доказательство. Сначала мы должны показать, что множество 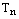 замкнуто относительно умножения. Пусть
замкнуто относительно умножения. Пусть 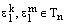 – два произвольных корня из 1, т.е.
– два произвольных корня из 1, т.е. 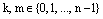 . Найдем их произведение:
. Найдем их произведение:
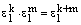 .
.
Замечаем, что
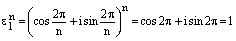 . (11)
. (11)
Отсюда следует, что 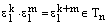 , если
, если 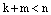 . В противном случае,
. В противном случае, 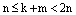 . Обозначим через
. Обозначим через 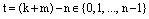 и
и 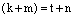 . Тогда
. Тогда
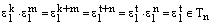 , ч.т.д.
, ч.т.д.
Таким образом, на множестве 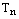 определена операция умножения и т.к. она ассоциативна и коммутативна в поле комплексных чисел, то она ассоциативна и коммутативна и на множестве
определена операция умножения и т.к. она ассоциативна и коммутативна в поле комплексных чисел, то она ассоциативна и коммутативна и на множестве 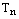 . Далее,
. Далее, 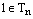 . Покажем, что любой элемент из
. Покажем, что любой элемент из 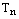 имеет обратный элемент также принадлежащий множеству
имеет обратный элемент также принадлежащий множеству 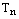 :
:
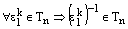 .
.
Действительно, по условию 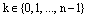 . Тогда
. Тогда
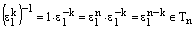 , т.е.
, т.е. 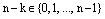 .
.
Теорема доказана.
Пример. Построить таблицу умножения для группы 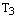 .
.
Решение. Обозначим для простоты
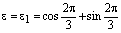 . Тогда
. Тогда 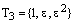 , где
, где 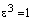 .
.
Заполняем таблицу Кэли (таблицу умножения):
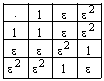
Изобразим все корни третьей степени из 1 на комплексной плоскости. Т.к. их модуль равен 1, то все они лежат на тригонометрической (т.е. единичной) окружности:
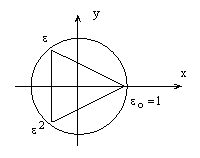
рис.3.
Здесь, 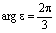 ,
, 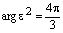 .
.
32. Многочлени. Дії над многочленами, теорема про ділення з остачею.
 2015-02-27
2015-02-27 1712
1712








