2015-02-27
1629
1. В линейном пространстве существует единственный нулевой вектор.
2. В линейном пространстве для любого вектора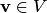 
существует единственный противоположный вектор 
.
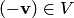3. Произведение произвольного вектора пространства на число нуль равно нулевому вектору, т.е.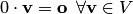 
.
4. Произведение нулевого вектора на любое число равно нулевому вектору, т.е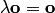 
для любого числа 
.
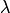5. Вектор, противоположный данному вектору, равен произведению данного вектора на число (-1), т.е.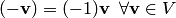 
.
6. В выражениях вида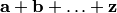 
(сумма конечного числа векторов) или 
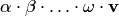(произведение вектора на конечное число множителей) можно расставлять скобки в любом порядке, либо вообще не указывать.
Докажем, например, первые два свойства. Единственность нулевого вектора. Есл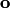и 
и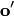 
— два нулевых вектора, то по аксиоме 3 получаем два равенства: 
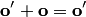или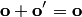 
, левые части которых равны по аксиоме 1. Следовательно, равны и правые части, т.е. 
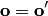. Единственность противоположного вектора. Если вектор 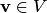имеет два противоположных вектора 
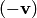и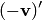 
, то по аксиомам 2, 3,4 получаем их равенство:
Остальные свойства доказываются аналогично.
