2015-02-27
629
1. Аксиомы 1-4 показывают, что линейное пространство является коммутативной группой относительно операции сложения.
2. Аксиомы 5 и 6 определяют дистрибутивность операции умножения вектора на число по отношению к операции сложения векторов (аксиома 5) или к операции сложения чисел (аксиома 6). Аксиома 7, иногда называемая законом ассоциативности умножения на число, выражает связь двух разных операций: умножения вектора на число и умножения чисел. Свойство, определяемое аксиомой 8, называется унитарностью операции умножения вектора на число.
3. Линейное пространство — это непустое множество, так как обязательно содержит нулевой вектор.
4. Операции сложения векторов и умножения вектора на число называются линейными операциями над векторами.
5. Разностью векторов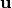 
и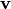 
называется сумма вектора 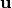с противоположным вектором 
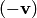и обозначается: 
.
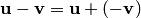6. Два ненулевых вектора 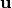и 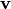называются коллинеарными (пропорциональными), если существует такое число 
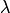, что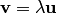 
. Понятие коллинеарности распространяется на любое конечное число векторов. Нулевой вектор 
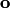считается коллинеарным с любым вектором.
|
|
|
