Алгебраические свойства векторного произведения

Для любых векторов 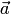, , 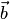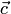и любого действительного числа :

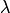1. ;

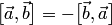2.;

3. .

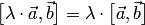Первое свойство определяет антисимметричность векторного произведения, второе и третье — аддитивность и однородность по первому множителю. Эти свойства аналогичны свойствам произведения чисел: первое свойство "противоположно" закону коммутативности умножения чисел (закон антикоммутативности), второе свойство соответствует закону дистрибутивности умножения чисел по отношению к сложению, третье — закону ассоциативности умножения. Поэтому рассматриваемая операция и называется произведением векторов. Поскольку ее результатом является вектор, то такое произведение векторов называется векторным.

Докажем первое свойство, предполагая, что векторы 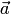и 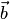не коллинеарны (в противном случае обе части доказываемого равенства равны нулевому вектору). По определению векторы 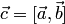и 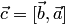имеют равные длины 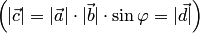и коллинеарны (так как оба вектора перпендикулярны одной плоскости). По определению тройки векторов 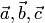и 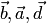— правые, т.е. вектор 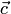направлен так, что кратчайший поворот от 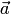к 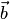происходит в положительном направлении (против часовой стрелки), если смотреть из конца вектора 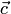, а вектор 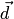направлен так, что кратчайший поворот от 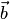к 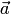происходит в положительном направлении, если смотреть из конца вектора 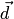(рис. 1.43). Это означает, что векторы 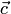и 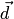противоположно направлены. Следовательно, 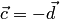, что и требовалось доказать. Доказательство остальных свойств приведено ниже (см. пункт 1 замечаний 1.13).