Вектор 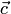 называется векторным произведением неколлинеарных векторов
называется векторным произведением неколлинеарных векторов 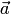 и
и 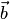 , если:
, если:
1) его длина равна произведению длин векторов 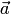 и
и 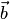 на синус угла между ними:
на синус угла между ними: 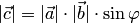 (рис.1.42);
(рис.1.42);

2) вектор 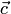 ортогонален векторам
ортогонален векторам 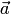 и
и 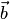 ;
;
3) векторы 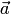 ,
, 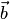 ,
, 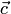 (в указанном порядке) образуют правую тройку.
(в указанном порядке) образуют правую тройку.
Векторное произведение коллинеарных векторов (в частности, если хотя бы один из множителей — нулевой вектор) считается равным нулевому вектору.
Векторное произведение обозначается 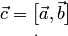 (или
(или 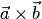 ).
).
 2015-02-27
2015-02-27 407
407







