1. Модуль векторного произведения численно равен площади параллелограмма, построенного на множителях (рис. 1.42,6).
2. Векторное произведение равняется нулевому вектору тогда и только тогда, когда множители коллинеарны, т.е.
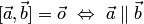 , в частности,
, в частности, 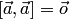 .
.
Первое свойство следует из определения. Докажем второе свойство. Равенство 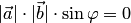 возможно в трех случаях:
возможно в трех случаях:  , или
, или 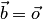 , или
, или 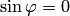 . В каждом из этих случаев векторы
. В каждом из этих случаев векторы 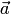 и
и 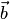 коллинеарны (см. разд. 1.1).
коллинеарны (см. разд. 1.1).

Пример 1.19. Вычислить площади параллелограмма и треугольника, построенных на векторах 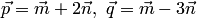 , где
, где 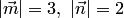 , угол между векторами
, угол между векторами 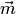 и
и 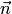 равен
равен 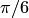 (рис. 1.44).
(рис. 1.44).
Решение. Используя алгебраические свойства, найдем сначала векторное произведение
а затем его модуль.
По первому геометрическому свойству векторного произведения искомая площадь параллелограмма равна 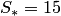 , а площадь треугольника в 2 раза меньше:
, а площадь треугольника в 2 раза меньше: 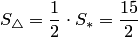 .
.
 2015-02-27
2015-02-27 915
915








