Геометрический смысл смешанного произведения

Выясним геометрический смысл смешанного произведения векторов 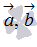и .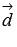

Отложим векторы 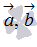и 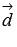от одной точки и построим параллелепипед на этих векторах как на сторонах.

Обозначим 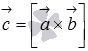. В этом случае смешанное произведение можно записать как 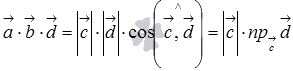, где 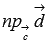- числовая проекция вектора 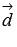на направление вектора .

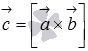Абсолютная величина числовой проекции 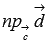равна высоте параллелепипеда, построенного на векторах 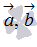и 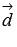, так как вектор 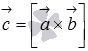перпендикулярен и вектору 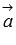и вектору 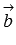по определению векторного произведения. А в разделе геометрический смысл векторного произведения мы выяснили, что величина 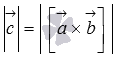представляет собой площадь параллелограмма, построенного на векторах 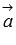и 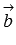. Таким образом, модуль смешанного произведения 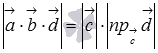- это произведение площади основания на высоту параллелепипеда, построенного на векторах 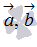и .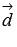

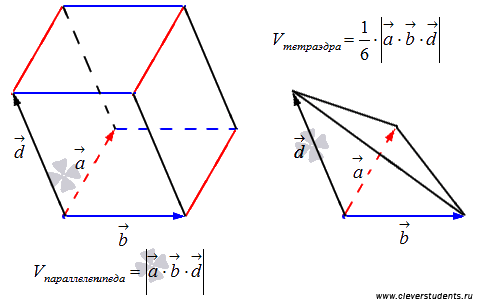
Следовательно, абсолютная величина смешанного произведения векторов представляет собой объем параллелепипеда: . В этом заключается геометрический смысл смешанного произведения векторов.

Объем тетраэдра, построенного на векторах 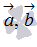и 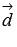, равен одной шестой объема соответствующего параллелепипеда, таким образом, .

Рассмотрим решения нескольких примеров.

Пример.

Вычислите объем параллелепипеда, построенного на векторах 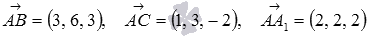, заданных в прямоугольной системе координат.

Решение.

Искомый объем параллелепипеда равен абсолютной величине смешанного произведения заданный векторов. Находим смешанное произведение:

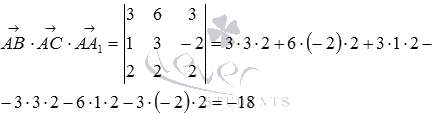
Тогда, .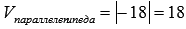

Ответ:

.

Пример.

В прямоугольной декартовой системе координат даны четыре точки 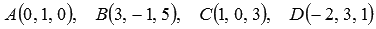. Найдите объем тетраэдра АВСD.

Решение.

Объем тетраэдра АВСD мы можем вычислить с использованием смешанного произведения векторов по формуле .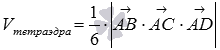

Найдем координаты векторов по координатам точек

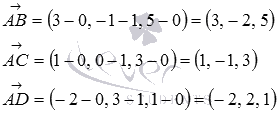
Вычисляем смешанное произведение 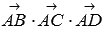по координатам векторов:

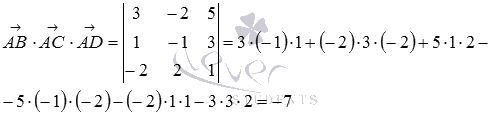
Таким образом, искомый объем тетраэдра равен .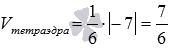

Ответ:

.

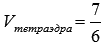Необходимое и достаточное условие компланарности трех векторов.

Напомним определение компланарных векторов.

Определение.

Векторы называются компланарными, если они принадлежат одной или параллельным плоскостям.

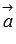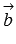Два вектора и трехмерного пространства всегда компланарны. Это утверждение легко доказать. Пусть a и b – прямые, на которых лежат векторы 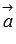и 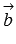соответственно. Проведем через начало вектора 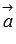прямую b₁, параллельную прямой b, а через начало вектора 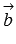прямую a₁, праллельную прямой a. Плоскости, образуемые прямыми a и b₁, а так же прямыми b и a₁, параллельны по построению, а векторы 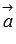и 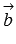принадлежат им. Следовательно, векторы 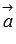и 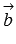компланарны.

А как же определить, являются ли три вектора компланарными?

Для этого существует необходимое и достаточное условие компланарности трех векторов в пространстве. Оно основано на понятии смешанного произведения векторов. Сформулируем его в виде теоремы.

Теорема.

Для компланарности трех векторов 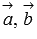и 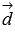трехмерного пространства необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.

Доказательство.

Пусть 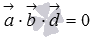, докажем что векторы 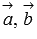и 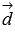компланарны.

Так как 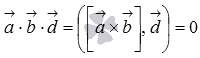, то векторы 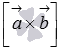и 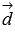перпендикулярны в силу необходимого и достаточного условия перпендикулярности двух векторов. С другой стороны, по определению векторного произведения вектор 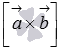перпендикулярен и вектору 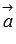и вектору 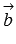. Следовательно, векторы 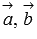и 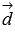компланарны, так как перпендикулярны одному вектору .

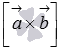Пусть теперь векторы 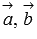и 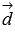компланарны, докажем равенство нулю смешанного произведения .

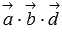Так как векторы 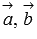и 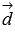компланарны, то вектор 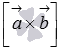перпендикулярен каждому из них, следовательно, скалярное произведение вектор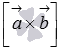а на 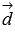равно нулю, что означает равенство нулю смешанного произведения .

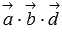Итак, теорема полностью доказана.

Покажем применение доказанного условия компланарности трех векторов к решению задач.

Пример.

Компланарны ли векторы 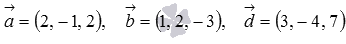, заданные в прямоугольной системе координат.

Решение.

Вычислим их смешанное произведение по координатам:

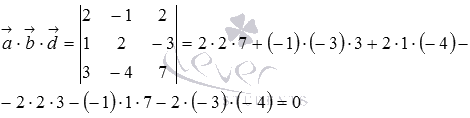
Так как мы получили ноль, то условие компланарности выполнено, следовательно, заданные векторы компланарны.

Ответ:

векторы компланарны.

Необходимое и достаточное условие компланарности векторов можно использовать для проверки принадлежности четырех точек пространства А, В, С и D одной плоскости. Для этого находим координаты векторов 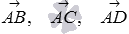и вычисляем их смешанное произведение. Если оно равно нулю, то точки лежат в одной плоскости, в противном случае – не лежат в одной плоскости.

Пример.

Принадлежат ли точки 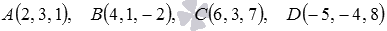одной плоскости?

Решение.

Найдем координаты векторов 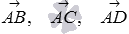(при необходимости смотрите статьюнахождение координат вектора по координатам точек его начала и конца):

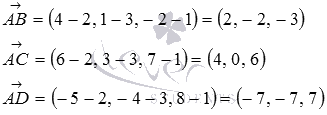
Теперь вычисляем смешанное произведение этих векторов

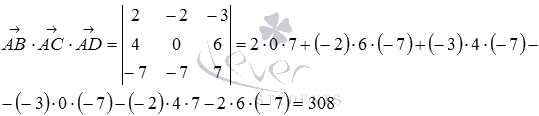
Так как смешанное произведение векторов отлично от нуля, то векторы 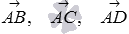не компланарны, следовательно, точки А, В, С и D не лежат в одной плоскости.

Ответ:

не принадлежат.

К началу страницы

52. Рівняння поверхні у просторі. Різні рівняння площин: загальне, неповні рівняння площин, у відрізках, рівняння площини, що проходить через три задані точки, нормальне рівняння площини.