2015-02-27
463
Из свойств векторного произведения и свойств скалярного произведения следуют следующие свойства смешанного произведения:
1.
;
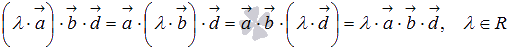2.
;
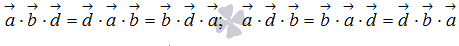3.
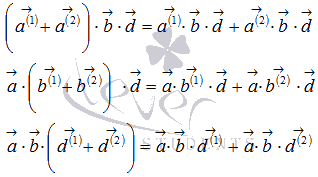
Очевидно, что если хотя бы один из умножаемых векторов нулевой, то смешанное произведение равно нулю.
Смешанное произведение также равно нулю, если хотя бы два умножаемых вектора равны.
Действительно, если 
, то по определению векторного произведения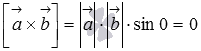 
, следовательно, смешанное произведение равно нулю, так как 
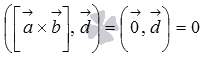. Если же или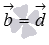 
, то угол между векторами 
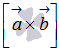и 
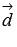равен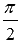 
, следовательно, по определению скалярного произведения векторов 
.
Свойства смешанного произведения обычно применяются при доказательстве тождеств или неравенств.
Рассмотрим несколько характерных задач.
Пример.
Докажите равенство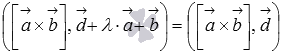 
, где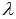 
- некоторое действительное число.
Решение.
Преобразуем левую часть равенства, обратившись к третьему свойству смешанного произведения:
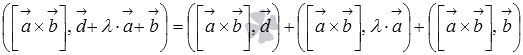
Выше мы показали, что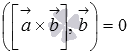 
, следовательно,
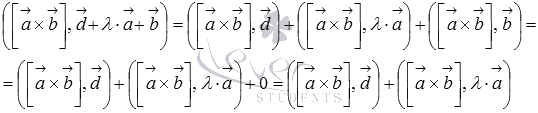
По первому свойству смешанного произведения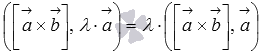 
, а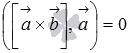 
. Таким образом, 
.
|
|
|
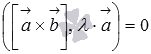Поэтому,
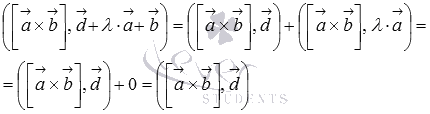
Что и требовалось доказать.
Пример.
Докажите, что модуль смешанного произведения трех векторов не превосходит произведения длин этих векторов.
Решение.
Иными словами, нам требуется доказать неравенство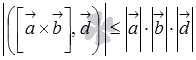 
.
По определению скалярного и векторного произведения векторов, мы можем записать
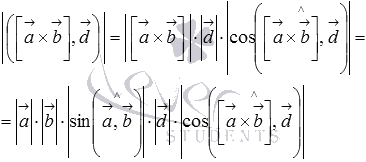
Из свойств основных элементарных функций мы знаем, что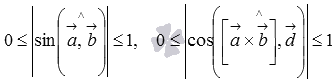 
. Следовательно,
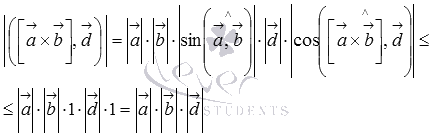
что и требовалось доказать.
К началу страницы
