Уравнение поверхности

В школе изучались уравнения линий на плоскости. В пространстве мы будем пользоваться уравнениями поверхностей и линий. Уточним сейчас, что такое уравнение поверхности.

Определение 11.1 Пусть в пространстве задана некоторая система координат и поверхность 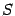. Будем говорить, что уравнение, связывающее три упорядоченные переменные, является уравнением поверхности 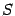в заданной системе координат, если координаты любой точки поверхности 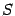удовлетворяют этому уравнению, а координаты любой точки, не лежащей на поверхности 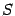, этому уравнению не удовлетворяют.

Вместо слов "координаты точки удовлетворяют уравнению" иногда будем говорить "точка удовлетворяет уравнению".

Если мы изменим систему координат, то, как правило, изменится и уравнение поверхности.

Если уравнение достаточно сложное, то удовлетворяющие ему точки могут образовывать не только поверхность, но и другие множества, например, линию, одну точку, пару линий. Есть такие уравнения, которым не удовлетворяет ни одна точка пространства. Например, ни одна точка с координатами 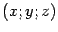не удовлетворяет уравнению .

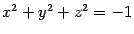В определении сказано, что уравнение должно связывать три переменных, но по записи уравнения не всегда можно определить, сколько переменных оно связывает. Например, уравнение 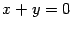можно рассматривать как уравнение прямой на плоскости, но можно это же уравнение записать в виде 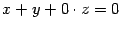, и тогда оно будет определять поверхность в пространстве (плоскость, как станет известно дальше). Поэтому кроме самого уравнения должна быть задана информация о том, в пространстве какой размерности находится определяемое этим уравнением множество точек.

Одна и та же поверхность может задаваться разными уравнениями. Например, если в уравнении поверхности 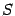в правой части стоит нуль: 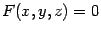, то обе части уравнения можно возвести в квадрат и получить 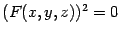. Новое уравнение будет являться уравнением той же самой поверхности 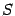, хотя будет выглядеть по другому. Естественно, что когда говорят об уравнении поверхности, то из всех уравнений этой поверхности стараются выбрать наиболее "простое Уравнение плоскости.

Определение. Плоскость - есть поверхность, полностью содержащая, каждую прямую, соединяющую любые её точки.