Проще всего смешанное произведение находится, когда известны координаты векторов. Для вычисления используется формула 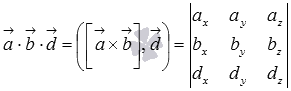 .
.
Пример.
Даны координаты трех векторов в прямоугольной системе координат 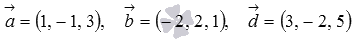 . Найдите смешанное произведение
. Найдите смешанное произведение 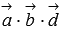 .
.
Решение.
Мы выяснили, что смешанное произведение векторов может быть вычислено через определитель матрицы третьего порядка, строками которой являются координаты векторов, то есть,
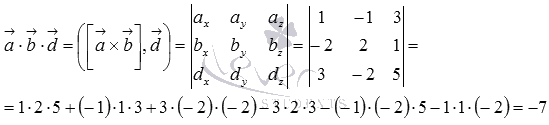
Ответ:
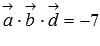 .
.
Пример.
Найдите векторно-скалярное произведение векторов  , где
, где 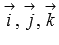 - орты прямоугольной декартовой системы координат.
- орты прямоугольной декартовой системы координат.
Решение.
Данные векторы имеют следующие координаты (при необходимости смотрите статьюкоординаты вектора в прямоугольной системе координат)
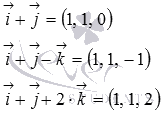
Осталось воспользоваться формулой для вычисления смешанного произведения через координаты векторов
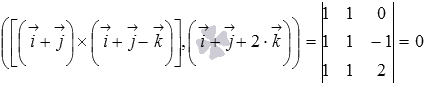
Ответ:
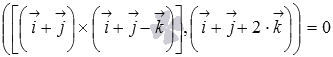 .
.
Смешанное произведение векторов также может быть вычислено, если известны длины векторов и углы между ними. Рассмотрим решение характерного примера.
Пример.
В правой прямоугольной декартовой системе координат заданы три взаимно перпендикулярных вектора  и
и  , образующих правую тройку, их длины равны соответственно 4, 2 и 3. Найдите их смешанное произведение
, образующих правую тройку, их длины равны соответственно 4, 2 и 3. Найдите их смешанное произведение 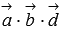 .
.
Решение.
Обозначим 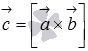 .
.
Нам известно, что скалярное произведение векторов равно произведению их длин на косинус угла между ними, поэтому 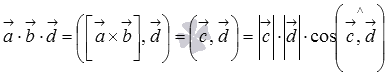 .
.
Сразу подставим значение длины вектора 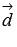 , известное из условия:
, известное из условия: 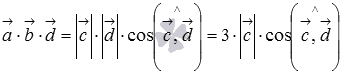 .
.
У нас остались неизвестные 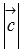 и
и  . Найдем их.
. Найдем их.
По условию 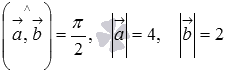 , тогда по определению векторного произведения находим длину вектора
, тогда по определению векторного произведения находим длину вектора 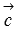 :
:
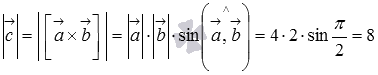
Из определения векторного произведения мы можем заключить, что вектор 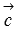 перпендикулярен вектору
перпендикулярен вектору 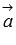 и вектору
и вектору 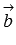 , причем тройка векторов
, причем тройка векторов 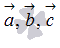 будет правой, так как векторы
будет правой, так как векторы 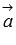 и
и 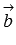 заданы в правой прямоугольной декартовой системе координат. Следовательно, векторы
заданы в правой прямоугольной декартовой системе координат. Следовательно, векторы 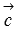 и
и 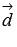 будут сонаправленными, то есть,
будут сонаправленными, то есть, 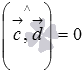 .
.
Подставляем полученные результаты и получаем искомое смешанное произведение: 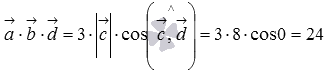 .
.
Ответ:
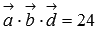
 2015-02-27
2015-02-27 2109
2109








